搜索
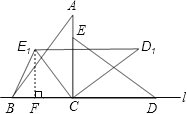
【题目】如图，直线l上摆放着两块大小相同的直角三角形△ABC和△ECD，∠ACB=∠DCE=90°，且BC=CE=3，AC=CD=4，将△ECD绕点C逆时针旋转到△E1CD1位置，且D1E1∥l ，则B、E1两点之间的距离为___________.
参考答案：
【答案】
【解析】过E1作E1F⊥BC，D1E1 与AC交于点O，如图：
∵D1E1∥l，∠DCE=90°，∴CO为△E1CD1的高，在△E1CD1中，BC=CE=CE1=3，AC=CD=CD1=4，
根据勾股定理得：D1E1=5，根据直角三角形面积公式
CE1CD1=
D1E1CO，解得：CO=
=E1F，
在Rt△CE1F中，利用勾股定理得：
，解得：CF=
，∴BF=BC-CF=3-
=
，
在Rt△BFE1中，利用勾股定理得：
，解得：
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】太阳是炽热巨大的气体星球，正以每秒
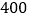万吨的速度失去重量．太阳的直径约为
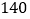万千米，而地球的半径约为
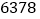千米．请将上述三个数据用科学记数法表示，然后计算：（1）在一年内太阳要失去多少万吨重量？
（2）在太阳的直径上能摆放多少个地球？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将两块三角板的顶点重合．
（1）请写出图中所有以
点为顶点且小于平角的角；（2）你写出的角中相等的角有________；
（3）若
，试求
的度数；（4）当三角板
绕点适当旋转（保持两三角板有重合部分）时，与
之间具有怎样的数量关系？
-
科目： 来源： 题型：
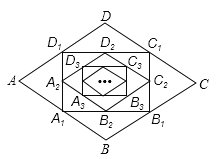
查看答案和解析>>【题目】如图，在菱形ABCD中，边长为10，∠A=60°，顺次连接菱形ABCD各边中点，可得四边形A1B1C1D1；顺次连结四边形A1B1C1D1各边中点，可得四边形A2B2C2D2；顺次连结四边形A2B2C2D2各边中点，可得四边形A3B3C3D3；按此规律继续下去…．则四边形A2B2C2D2的周长是 ；四边形A2015B2015C2015D2015的周长 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，分别以AC，BC为边作等边△ACD和等边△BCE．设△ACD、△BCE、△ABC的面积分别是S1、S2、S3 ， 现有如下结论：
①S1：S2=AC2：BC2；
②连接AE，BD，则△BCD≌△ECA；
③若AC⊥BC，则S1S2=
S32 ．
其中结论正确的序号是 ．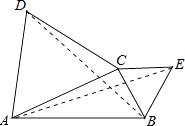
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校积极开展每天锻炼1小时活动，老师对本校八年级学生进行一分钟跳绳测试，并对跳绳次数进行统计，绘制了八(1)班一分钟跳绳次数的频数分布直方图和八年级其余班级一分钟跳绳次数的扇形统计图.已知在图1中，组中值为150次一组的 频率为0.2.（说明: 组中值为190次的组别为 180≤次数＜200）
请结合统计图完成下列问题：
（1）八(1)班的人数是 ，组中值为110次一组的频率为 ；
（2）请把频数分布直方图补充完整；
（3）如果一分钟跳绳次数不低于120次的同学视为达标，八年级同学一分钟跳绳的达标率不低于90％，那么八年级同学至少有多少人？请写出解答过程。
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交与BE的延长线于点F，且AF=DC，连结CF．
（1）求证：四边形ADCF是平行四边形；
（2）当AB与AC有何数量关系时，四边形ADCF为矩形，请说明理由．
相关试题
