【题目】如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是 . 
参考答案:
【答案】![]()
【解析】解:作E点关于AC对称点E′点,连接E′B,E′B与AC的交点即是P点,
∵菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,
∴AE′=AE=BE=1,
∴△AEE′为等边三角形,
∴∠AEE′=60°,
∴∠E′EB=120°,
∵BE=EE′,
∴∠EE′B=30°,
∴∠AE′B=90°,
BE′= ![]() =
= ![]() ,
,
∵PE+PB=BE′,
∴PE+PB的最小值是: ![]() .
.
故答案为: ![]() .
.
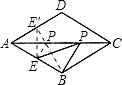
根据轴对称最短问题作法首先求出P点的位置,再结合菱形的性质得出△AEE′为等边三角形,进而求出PE+PB的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及S四边形ABDC.
(2)在y轴上是否存在一点Q,连接QA,QB,使S△QAB=S四边形ABDC?若存在这样一点,求出点Q的坐标;若不存在,试说明理由.
(3)如图②,点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合),给出下列结论:①
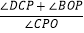 的值不变,②
的值不变,②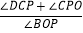 的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.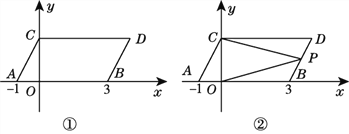
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知经过原点的抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=﹣1,下列结论中: ①ab>0,②a+b+c>0,③当﹣2<x<0时,y<0.
正确的个数是( )
A.0个
B.1个
C.2个
D.3个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是连续十周测试甲、乙两名运动员体能情况的折线统计图,教练组规定:体能测试成绩70分以上(包括70分)为合适.
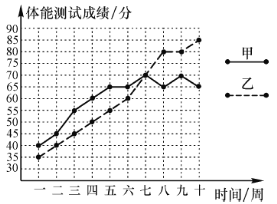
(1)请根据图中所提供的信息填写下表:
平均数
中位数
体能测试成绩合格次数(次)
甲
65
乙
60
(2)请从下面两个不同的角度对运动员体能测试结果进行判断:①依据平均数与成绩合格的次数比较甲和乙,哪个的体能测试成绩较好;②依据平均数与中位数比较甲和乙,哪个的体能测试成绩较好;
(3)依据折线统计图和成绩合格的次数,分析哪位运动员体能训练的效果较好.
-
科目: 来源: 题型:
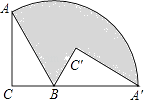
查看答案和解析>>【题目】将直角△ABC绕顶点B旋转至如图位置,其中∠C=90°,AB=4,BC=2,点C、B、A′在同一直线上,则阴影部分的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)3x﹣1=2﹣x;
(2)1﹣2(x﹣1)=﹣3x;
(3)
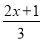 ﹣
﹣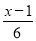 =1;
=1;(4)
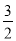 [2(x﹣
[2(x﹣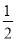 )+
)+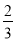 ]=5x.
]=5x. -
科目: 来源: 题型:
查看答案和解析>>【题目】作图:在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形.按要求画出下列图形:
(1)将△ABC向右平移5个单位得到△A′B′C′;
(2)将△A′B′C′绕点A′顺时针旋转90°得到△A′DE;
(3)连结EC′,则△A′EC′是 三角形.

相关试题

