搜索
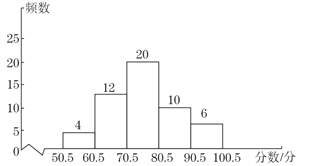
【题目】某校举办以“保护环境，治理雾霾，从我做起”为主题的演讲比赛，现将所有比赛成绩(得分取整数，满分为100分)进行整理后分为5组，并绘制成如图所示的频数直方图．根据频数分布直方图提供的信息，下列结论：①参加比赛的学生共有52人；②比赛成绩为65分的学生有12人；③比赛成绩的中位数落在70.5～80.5分这个分数段；④如果比赛成绩在80分以上(不含80分)可以获得奖励，则本次比赛的获奖率约为30.8%.正确的是________．(把所有正确结论的序号都填在横线上)
参考答案：
【答案】①③④
【解析】试题解析：参赛学生共有
人，所以①正确；根据频数直方图，比赛成绩在60.5-70.5分段的学生有12人，故②错误；因为参赛人数为52人，那么中位数应为第26、27名成绩的平均数，由频数分布图，第26、27名的成绩在70.5-80.5分段内，所以中位数落在70.5-80.5分段，故③正确；比赛成绩在80分以上的人数为16人，则获奖率为
，故④正确.
所以本题的正确答案为①③④.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，∠1＝∠2，则不一定能使△ABD≌△ACD的条件是 （ ）
A. AB＝AC B. BD＝CD C. ∠B＝∠C D. ∠BDA＝∠CDA
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，边长为2的正五边形ABCDE内接于⊙O，AB、DC的延长线交于点F，过点E作EG∥CB交BA的延长线于点G．
（1）求证：
；
（2）证明：EG与⊙O相切，并求AG、BF的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】今年，我省启动了“关爱留守儿童工程”．某村小为了了解各年级留守儿童的数量，对一到六年级留守儿童数量进行了统计，得到每个年级的留守儿童人数分别为10，15，10，17，18，20．对于这组数据，下列说法错误的是（ ）
A．平均数是15 B．众数是10 C．中位数是17 D．方差是
-
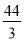
科目： 来源： 题型：
查看答案和解析>>【题目】如图，是交警在一个路口统计的某个时段来往车辆的车速(单位：km/h)．
（1）计算这些车的平均速度．
（2）车速的众数是多少？
（3）车速的中位数是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD是⊙O的内接正方形，延长BA到E，使AE=AB，连接ED．
（1）求证：直线ED是⊙O的切线；
（2）连接EO交AD于点F，求证：EF=2FO． -
科目： 来源： 题型：
查看答案和解析>>【题目】（1）抛物线
经过点A (4，0)，点B (1，－3) ，求该抛物线的解析式；(2)如图，要修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高，高度为3m，水柱落地处离池中心3m，水管应多长？
（3）如图，点P
（
＞0），在
轴正半轴上，过点P作平行于
轴的直线，分别交抛物线
于点A，B，交抛物线
于点C，D，求
的值.
相关试题
