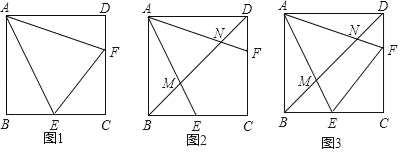
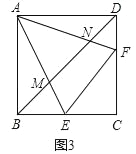
【题目】已知E、F分别为正方形ABCD的边BC、CD上的点,且∠EAF=45°.
(1)如图①求证:BE+DF=EF;
(2)连接BD分别交AE、AF于M、N,
①如图②,若AB=6![]() ,BM=3,求MN.
,BM=3,求MN.
②如图③,若EF∥BD,求证:MN=CE.
参考答案:
【答案】(1)证明见解析;(2)①5;②证明见解析.
【解析】
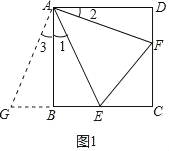
(1)延长CB到G,使GB=DF,连接AG,求证△ABG≌△ADF,得∠3=∠2,AG=AF,进而求证△AGE≌△AFE,可得GB+BE=EF,所以DF+BE=EF.
(2)①如图2,把△ABM绕点A逆时针旋转90°得到△ADM′,连接NM′.就可以得出△ABM≌△ADM′,就有∠BAM=∠DAM′,就可以得出△AMN≌△AM′N就可以得出MN=M′N,由勾股定理就可以得出结论MN2=DN2+BM2;
②设正方形ABCD的边长为a,求出MN,EC即可判断;
(1)证明:证明:延长CB到G,使GB=DF,连接AG(如图1),
∵AB=AD,∠ABG=∠D=90°,GB=DF,
∴△ABG≌△ADF(SAS),
∴∠3=∠2,AG=AF,
∵∠BAD=90°,∠EAF=45°,
∴∠1+∠2=45°,
∴∠GAE=∠1+∠3=45°=∠EAF,
∵AE=AE,∠GAE=∠EAF,AG=AF,
∴△AGE≌△AFE(SAS),
∴GB+BE=EF,
∴DF+BE=EF;
(2)①解:如图2,在正方形ABCD中,AB=AD,∠BAD=90°,
∴∠ABM=∠ADN=45°.
把△ABM绕点A逆时针旋转90°得到△ADM'.连结NM'.
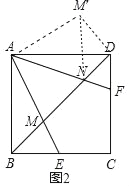
∴△ABM≌△ADM′(旋转不变性),
∴DM'=BM,AM'=AM,∠ADM'=∠ABM=45°,∠DAM'=∠BAM.
∴∠ADB+∠ADM′=45°+45°=90°,
即∠NDM′=90°.
∵∠EAF=45°,
∴∠BAM+∠DAN=45°,
∴∠DAM′+∠DAF=45°,
即∠M′AN=45°,
∴∠M'AN=∠MAN.
在△AMN和△AM′N中
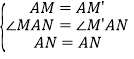 ,
,
∴△AMN≌△AM′N(SAS),
∴M'N=MN.
∵∠NDM′=90°,
∴M'N2=DN2+DM'2,
∴MN2=DN2+BM2;
设MN=x,则DN=12﹣3﹣x=9﹣x,
∴x2=33+(9﹣x)2,
∴x=5,
∴NM=5;
②证明:如图3中,设正方形ABCD的边长为a.
∵EF∥BD,
∴∠CEF=∠CBD=45°,∠CFE=∠CDB=45°,
∴∠CEF=∠CFE=45°,
∴CE=CF,
∴BE=DF,
∵AB=AD,∠ABE=∠ADF,BE=DF,
∴△ABE≌△ADF(SAS),
∴∠BAE=∠DAF,
∵∠EAF=45°,
∴∠BAE=∠DAF=22.5°,
∴∠AEB=∠BME=67.5°,
∴BM=BE,同理可证:DN=DF,
∴BM=DN=BE=DF,设BM=x,则MN=![]() x,
x,
∴2x+![]() x=
x=![]() a,
a,
∴x=(![]() ﹣1)a,
﹣1)a,
∴MN=(2﹣![]() )a,EC=BC﹣BE=(2﹣
)a,EC=BC﹣BE=(2﹣![]() )a,
)a,
∴MN=EC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】高新一中新图书馆在“校园书香四溢”活动中迎来了借书高潮,上周借书记录如下表:(超过100册的部分记为正,少于100册的部分记为负)
(1)上星期借书最多的一天比借书最少的一天多借出图书多少册?
(2)上星期平均每天借出多少册书?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD绕点A按逆时针方向旋转,得到矩形AEFG,E点正好落在边CD上,连接BE,BG,且BG交AE于P.
(1)求证:∠CBE=
 ∠BAE;
∠BAE;(2)求证:PG=PB;
(3)若AB=
 ,BC=3,求出BG的长.
,BC=3,求出BG的长. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中,不能确定ABC 是直角三角形的条件是( )
A.A
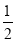 B=
B=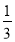 CB.A 2B 3C
CB.A 2B 3CC.A B
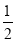 CD.A 2B 2C
CD.A 2B 2C -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学在一次用频率去估计概率的实验中统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的实验可能是( )
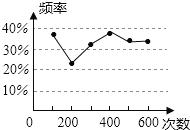
A.从一装有2个白球和1个红球的袋子中任取一球,取到红球的概率
B.掷一枚正六面体的骰子,出现1点的概率
C.抛一枚硬币,出现正面的概率
D.任意写一个整数,它能被2整除的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个小组同时从甲地出发,匀速步行到乙地,甲乙两地相距7500米,第一组的步行速度是第二组的1.2倍,并且比第二组早15分钟到达乙地,设第二组的步行速度为x千米/小时,根据题意可列方程是( ).
A.
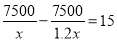 B.
B.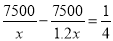
C.
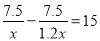 D.
D.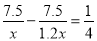
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,等腰
 中,
中, ,
, 是高
是高 上任一点,
上任一点, 是腰
是腰 上任一点,腰
上任一点,腰 ,
, ,
, ,那么线段
,那么线段 的最小值是____________.
的最小值是____________.
相关试题

