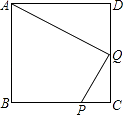
【题目】在正方形ABCD中,P是BC上一点,且BP=3PC,Q是CD得中点. 
(1)证明△ADQ∽△QCP;
(2)求证:AQ⊥QP.
参考答案:
【答案】
(1)证明:∵BP=3PC,Q是CD的中点
∴ ![]() =
= ![]() ,又∵∠ADQ=∠QCP=90°,
,又∵∠ADQ=∠QCP=90°,
∴△ADQ∽△QCP
(2)证明:∵△ADQ∽△QCP,
∴∠AQD=∠QPC,∠DAQ=∠PQC,
∴∠PQC+∠DQA=∠DAQ+∠AQD=90°,
∴AQ⊥QP
【解析】(1)根据BP=3PC和Q是CD的中点,可以求得 ![]() ,即可求证△ADQ∽△QCP;(2)根据△ADQ∽△QCP可以求得∠PQC+∠DQA=90°,即可解题.
,即可求证△ADQ∽△QCP;(2)根据△ADQ∽△QCP可以求得∠PQC+∠DQA=90°,即可解题.
【考点精析】本题主要考查了正方形的性质和相似三角形的判定与性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论: ①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+
 .
.
其中正确的序号是(把你认为正确的都填上).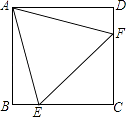
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:ABCD的两边AB,AD的长是关于x的方程x2﹣mx+
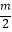 ﹣
﹣  的两个实数根.
的两个实数根.
(1)当m为何值时,ABCD是菱形?
(2)若AB的长为2,那么ABCD的周长是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】用A4纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元.
设在同一家复印店一次复印文件的页数为x(x为非负整数).
(1)根据题意,填写下表:
一次复印页数(页)
5
10
20
30
…
甲复印店收费(元)
0.5
2
…
乙复印店收费(元)
0.6
2.4
…
(2)设在甲复印店复印收费y1元,在乙复印店复印收费y2元,分别写出y1,y2关于x的函数关系式;
(3)当x>70时,顾客在哪家复印店复印花费少?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司投资新建了一商场,共有商铺30间.据预测,当每间的年租金定为10万元时,可全部租出.每间的年租金每增加5000元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5000元.
(1)当每间商铺的年租金定为13万元时,能租出多少间?
(2)当每间商铺的年租金定为多少万元时,该公司的年收益(收益=租金﹣各种费用)为275万元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD,BC于点E,F,垂足为点O.

(1)连接AF,CE,求证:四边形AFCE为菱形;
(2)求AF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明从家到图书馆看报,然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,试求:
(1)小明回家的速度.
(2)小明离家50分钟时离家的距离.

相关试题

