【题目】某校为了更好地开展球类运动,体育组决定用1600元购进足球8个和篮球14个,并且篮球的单价比足球的单价多20元,请解答下列问题:
(1)求出足球和篮球的单价;
(2)若学校欲用不超过3240元,且不少于3200元再次购进两种球50个,求出有哪几种购买方案?
(3)在(2)的条件下,若已知足球的进价为50元,篮球的进价为65元,则在第二次购买方案中,哪种方案商家获利最多?
参考答案:
【答案】
(1)解:设足球的单价为x元,则篮球的单价为(x+20)元,
根据题意,得8x+14(x+20)=1600,
解得:x=60,x+20=80.
即足球的单价为60元,则篮球的单价为80元;
(2)解:设购进足球y个,则购进篮球(50﹣y)个.
根据题意,得 ![]() ,
,
解得: ![]() ,
,
∵y为整数,
∴y=38,39,40.
当y=38,50﹣y=12;
当y=39,50﹣y=11;
当y=40,50﹣y=10.
故有三种方案:
方案一:购进足球38个,则购进篮球12个;
方案二:购进足球39个,则购进篮球11个;
方案三:购进足球40个,则购进篮球10个;
(3)解:商家售方案一的利润:38(60﹣50)+12(80﹣65)=560(元);
商家售方案二的利润:39(60﹣50)+11(80﹣65)=555(元);
商家售方案三的利润:40(60﹣50)+10(80﹣65)=550(元).
故第二次购买方案中,方案一商家获利最多
【解析】(1)设足球的单价为x元,则篮球的单价为(x+20)元,则根据所花的钱数为1600元,可得出方程,解出即可;(2)根据题意所述的不等关系:不超过3240元,且不少于3200元,等量关系:两种球共50个,可得出不等式组,解出即可;(3)分别求出三种方案的利润,继而比较可得出答案.
【考点精析】本题主要考查了一元一次不等式组的应用的相关知识点,需要掌握1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生零花钱的使用情况,校团委随机调查了本校部分学生每人一周的零花钱数额,并绘制了如图甲、乙所示的两个统计图(部分未完成).请根据图中信息,回答下列问题:

(1)校团委随机调查了多少学生?请你补全条形统计图;
(2)表示“50元”的扇形的圆心角是多少度?被调查的学生每人一周零花钱数额的中位数是多少元?
(3)为捐助贫困山区儿童学习,全校1000名学生每人自发地捐出一周的零花钱.请估算全校学生共捐款多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,
 是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是
是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是 ,当点P到达点B时,P、Q两点停止运动,设点P的运动时间
,当点P到达点B时,P、Q两点停止运动,设点P的运动时间 ,解答下列各问题:
,解答下列各问题: 经过
经过 秒时,求
秒时,求 的面积;
的面积; 当t为何值时,
当t为何值时,  是直角三角形?
是直角三角形? 是否存在某一时刻t,使四边形APQC的面积是
是否存在某一时刻t,使四边形APQC的面积是 面积的三分之二?如果存在,求出t的值;不存在请说明理由.
面积的三分之二?如果存在,求出t的值;不存在请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(a-b)2(a-b)3(b-a)5 (2)(a-b+c)3(b-a-c)5(a-b+c)6
(3)(b-a)m·(b-a)n-5·(a-b)5 (4)x·xm-1+x2·xm-2-3x3·xm-3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D落在AB边上,斜边DE交AC于点F,则n的大小和图中阴影部分的面积分别为( )

A. 30,2 B. 60,2 C. 60,
 D. 60,
D. 60,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( )
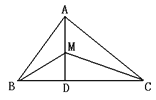
A. 9 B. 35 C. 45 D. 无法计算
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个有50个奇数排成的数阵,用如图所示的框去框住四个数,并求出这四个数的和,在下列给出的备选答案中,有可能是这四个数的和的是( )

A. 114 B. 122 C. 220 D. 84
相关试题

