【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D落在AB边上,斜边DE交AC于点F,则n的大小和图中阴影部分的面积分别为( )

A. 30,2 B. 60,2 C. 60,![]() D. 60,
D. 60,![]()
参考答案:
【答案】C
【解析】
先根据已知条件求出AC的长及∠B的度数,再根据图形旋转的性质及等边三角形的判定定理判断出△BCD的形状,进而得出∠DCF的度数,由直角三角形的性质可判断出DF是△ABC的中位线,由三角形的面积公式即可得出结论.
解答:解:∵△ABC是直角三角形,∠ACB=90°,∠A=30°,BC=2,
∴∠B=60°,AC=BC×cot∠A=2×![]() =2
=2![]() ,AB=2BC=4,
,AB=2BC=4,
∵△EDC是△ABC旋转而成,
∴BC=CD=BD=![]() AB=2,
AB=2,
∵∠B=60°,
∴△BCD是等边三角形,
∴∠BCD=60°,
∴∠DCF=30°,∠DFC=90°,即DE⊥AC,
∴DE∥BC,
∵BD=![]() AB=2,
AB=2,
∴DF是△ABC的中位线,
∴DF=![]() BC=
BC=![]() ×2=1,CF=
×2=1,CF=![]() AC=
AC=![]() ×2
×2![]() =
=![]() ,
,
∴S阴影=![]() DF×CF=
DF×CF=![]() ×
×![]() =
=![]() .
.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,
 是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是
是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是 ,当点P到达点B时,P、Q两点停止运动,设点P的运动时间
,当点P到达点B时,P、Q两点停止运动,设点P的运动时间 ,解答下列各问题:
,解答下列各问题: 经过
经过 秒时,求
秒时,求 的面积;
的面积; 当t为何值时,
当t为何值时,  是直角三角形?
是直角三角形? 是否存在某一时刻t,使四边形APQC的面积是
是否存在某一时刻t,使四边形APQC的面积是 面积的三分之二?如果存在,求出t的值;不存在请说明理由.
面积的三分之二?如果存在,求出t的值;不存在请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(a-b)2(a-b)3(b-a)5 (2)(a-b+c)3(b-a-c)5(a-b+c)6
(3)(b-a)m·(b-a)n-5·(a-b)5 (4)x·xm-1+x2·xm-2-3x3·xm-3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了更好地开展球类运动,体育组决定用1600元购进足球8个和篮球14个,并且篮球的单价比足球的单价多20元,请解答下列问题:
(1)求出足球和篮球的单价;
(2)若学校欲用不超过3240元,且不少于3200元再次购进两种球50个,求出有哪几种购买方案?
(3)在(2)的条件下,若已知足球的进价为50元,篮球的进价为65元,则在第二次购买方案中,哪种方案商家获利最多? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( )
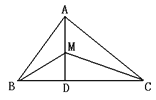
A. 9 B. 35 C. 45 D. 无法计算
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个有50个奇数排成的数阵,用如图所示的框去框住四个数,并求出这四个数的和,在下列给出的备选答案中,有可能是这四个数的和的是( )

A. 114 B. 122 C. 220 D. 84
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图的平面直角坐标系中有一个正六边形ABCDEF,其中C.D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A.B.C.D.E、F中,会过点(45,2)的是点 ▲ .

相关试题

