【题目】如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E. 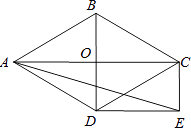
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2 ![]() 时,求sin∠AED的值.
时,求sin∠AED的值.
参考答案:
【答案】
(1)证明:∵DE∥AC,CE∥BD,
∴DE∥OC,CE∥OD,
∴四边形OCED是平行四边形,
又∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠COD=90°,
∴四边形OCED是矩形
(2)解:∵∠ADB=60°,AD=2 ![]() ,
,
∴OD= ![]() ,AO=3,
,AO=3,
∴CE= ![]() ,AC=6,
,AC=6,
由勾股定理得:AE= ![]() =
= ![]() =
= ![]() ,
,
∴sin∠AED=sin∠CAE= ![]()
![]() =
= ![]()
【解析】(1)根据平行四边形的判定得出边形OCED是平行四边形,根据菱形的性质求出∠COD=90°,根据矩形的判定得出即可;(2)解直角三角形求出AO、DO、求出AC、CE,根据勾股定理求出AE,解直角三角形求出即可.
-
科目: 来源: 题型:
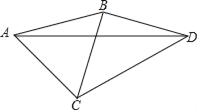
查看答案和解析>>【题目】如图,∠BAD=∠BDA=15°,∠CAD=45°,∠CDA=30°,试判断三角形ABC的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,河坝横断面背水坡AB的坡角是45°,背水坡AB长度为20
 米,现在为加固堤坝,将斜坡AB改成坡度为1:2的斜坡AD【备注:AC⊥CB】
米,现在为加固堤坝,将斜坡AB改成坡度为1:2的斜坡AD【备注:AC⊥CB】 
(1)求加固部分即△ABD的横截面的面积;
(2)若该堤坝的长度为100米,某工程队承包了这一加固的土石方工程,为抢在在汛期到来之际提前完成这一工程,现在每天完成的土方比原计划增加25%,这样实际比原计划提前10天完成了,求原计划每天完成的土方.【提示土石方=横截面x堤坝长度】 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个正方体的平面展开图,标注了A字母的是正方体的正面,如果正方体的左面与右面标注的式子相等.

(1)求x的值.
(2)求正方体的上面和底面的数字和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校“数学魔盗团”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B种魔方共需130元,购买1个A种魔方比1个B种魔方多花5元.

(1)求这两种魔方的单价;
(2)结合社员们的需求,社团决定购买A,B两种魔方共100个(其中A种魔方不超过50个).“双11期间”某商店有两种优惠活动,如图所示.请根据以上信息填空:购买A种魔方________个时选择活动一盒活动二购买所需费用相同.
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定:四条边对应相等,四个角对应相等的两个四边形全等.某学习小组在研究后发现判定两个四边形全等需要五组对应条件,于是把五组条件进行分类研究,并且针对二条边和三个角对应相等类型进行研究提出以下几种可能:
① AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1;
② AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠D=∠D1;
③ AB=A1B1,AD=A1D1,∠B=∠B1,∠C=∠C1,∠D=∠D1;
④ AB=A1B1,CD=C1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1.
其中能判定四边形ABCD和四边形A1B1C1D1全等有( )个

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】九年级(1)班的全体同学根据自己的兴趣爱好参加了六个学生社团(每个学生必须参加且只参加一个),为了了解学生参加社团的情况,学生会对该班参加各个社团的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“读书社”的学生有10人,请解答下列问题:

(1)该班的学生共有名;该班参加“爱心社”的人数为名,若该班参加“吉他社”与“街舞社”的人数相同,则“吉他社”对应扇形的圆心角的度数为;
(2)一班学生甲、乙、丙是“爱心社”的优秀社员,现要从这三名学生中随机选两名学生参加“社区义工”活动,请你用画树状图或列表的方法求出恰好选中甲和乙的概率.
相关试题

