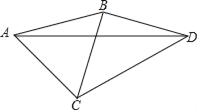
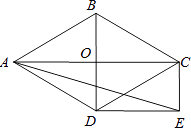
【题目】如图,∠BAD=∠BDA=15°,∠CAD=45°,∠CDA=30°,试判断三角形ABC的形状,并说明理由.
参考答案:
【答案】三角形ABC为等边三角形,理由详见解析.
【解析】
△ABC为等边三角形,将△ABC绕B点旋转,使A点与D点重合,得△ABC′,连接CC′,则得到△ABC≌△DBC′,再由角的关系及等腰三角形的性质证明△ACD≌△C′DC,△ABD≌△CBC′,得出∠∠ABC=60°,从而判定△ABC为等边三角形.
解:三角形ABC为等边三角形.
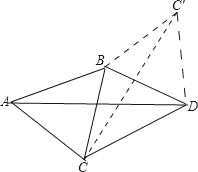
因此将△ABC绕B点旋转,使A点与D点重合,连接CC′,则△ABC≌△DBC′,
∴BC=BC′,AC=DC′,∠BDC′=∠BAC,∠ABC=∠DBC′,
∵∠BAD=∠BDA=15°,∠CAD=45°,∠CDA=30°,
∴∠CDC′=∠CDA+∠BDA+∠BDC′=∠CDA+∠BDA+∠ABC=∠CDA+∠BDA+∠CAD+∠BAD=30°+15°+45°+15°=105°,
∴∠ACD=180°-∠CAD-∠CDA=180°-45°-30°=105°,
又CD=CD,
∴△ACD≌△C′DC,
∴AD=CC′,
∠CBC′=∠DBC′+∠CBD,∠ABD=∠ABC+∠CBD,
∵∠ABC=∠DBC′,
∴∠CBC′=∠ABD=180°-15°-15°=150°,
∴∠BCC′=∠BC′C=15°,
∴△ABD≌△CBC′,
∴AB=BC,
∴∠ACB=∠BAC=∠BAD+∠CAD=15°+45°=60°,
∴∠ABC=60°,
∴△ABC为等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“两直线平行,内错角的平分线互相平行”是真命题吗?如果是,请给出证明;如果不是,请举出反例.
-
科目: 来源: 题型:
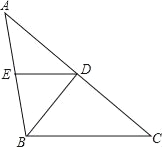
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,∠ABC=100°,BD是∠ABC的平分线,E是AB的中点.
(1)证明DE∥BC;(2)求∠EDB的度数.
-
科目: 来源: 题型:
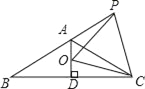
查看答案和解析>>【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC.
(1)求∠APO+∠DCO的度数;
(2)求证:点P在OC的垂直平分线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,河坝横断面背水坡AB的坡角是45°,背水坡AB长度为20
 米,现在为加固堤坝,将斜坡AB改成坡度为1:2的斜坡AD【备注:AC⊥CB】
米,现在为加固堤坝,将斜坡AB改成坡度为1:2的斜坡AD【备注:AC⊥CB】 
(1)求加固部分即△ABD的横截面的面积;
(2)若该堤坝的长度为100米,某工程队承包了这一加固的土石方工程,为抢在在汛期到来之际提前完成这一工程,现在每天完成的土方比原计划增加25%,这样实际比原计划提前10天完成了,求原计划每天完成的土方.【提示土石方=横截面x堤坝长度】 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个正方体的平面展开图,标注了A字母的是正方体的正面,如果正方体的左面与右面标注的式子相等.

(1)求x的值.
(2)求正方体的上面和底面的数字和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2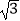 时,求sin∠AED的值.
时,求sin∠AED的值.
相关试题

