【题目】九年级(1)班的全体同学根据自己的兴趣爱好参加了六个学生社团(每个学生必须参加且只参加一个),为了了解学生参加社团的情况,学生会对该班参加各个社团的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“读书社”的学生有10人,请解答下列问题: 
(1)该班的学生共有名;该班参加“爱心社”的人数为名,若该班参加“吉他社”与“街舞社”的人数相同,则“吉他社”对应扇形的圆心角的度数为;
(2)一班学生甲、乙、丙是“爱心社”的优秀社员,现要从这三名学生中随机选两名学生参加“社区义工”活动,请你用画树状图或列表的方法求出恰好选中甲和乙的概率.
参考答案:
【答案】
(1)40;8;36°
(2)解:画树状图如下:

共有8种等可能的结果数,其中恰好选中甲和乙的情况有2种,
所以P(选中甲和乙)= ![]() =
= ![]()
【解析】解:(1)因为参加“读书社”的学生有10人,且在扇形统计图中,所占比例为25%, 所以该班的学生共有10÷25%=40(人);
该班参加“爱心社”的人数=40×20%=8(名);
参加“吉他社”的学生在全班学生中所占比为 ![]() (1﹣25%﹣15%﹣20%﹣20%)=10%,
(1﹣25%﹣15%﹣20%﹣20%)=10%,
所以“吉他社”对应扇形的圆心角的度数为:360°×10%=36°;
故答案为40,8,36°;
(1)利用参加“读书社”的学生数和它所占比例可计算出调查的学生总数,再用学生总数乘以“爱心社”所占的百分比得到该班参加“爱心社”的人数,然后计算出该班参加“吉他社”的百分比,用此百分比乘以360度即可得到“吉他社”对应扇形的圆心角的度数;(3)画树状图展示所有8种等可能的结果数,再找出恰好选中甲和乙的结果数,然后根据概率公式求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
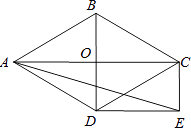
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2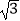 时,求sin∠AED的值.
时,求sin∠AED的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校“数学魔盗团”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B种魔方共需130元,购买1个A种魔方比1个B种魔方多花5元.

(1)求这两种魔方的单价;
(2)结合社员们的需求,社团决定购买A,B两种魔方共100个(其中A种魔方不超过50个).“双11期间”某商店有两种优惠活动,如图所示.请根据以上信息填空:购买A种魔方________个时选择活动一盒活动二购买所需费用相同.
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定:四条边对应相等,四个角对应相等的两个四边形全等.某学习小组在研究后发现判定两个四边形全等需要五组对应条件,于是把五组条件进行分类研究,并且针对二条边和三个角对应相等类型进行研究提出以下几种可能:
① AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1;
② AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠D=∠D1;
③ AB=A1B1,AD=A1D1,∠B=∠B1,∠C=∠C1,∠D=∠D1;
④ AB=A1B1,CD=C1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1.
其中能判定四边形ABCD和四边形A1B1C1D1全等有( )个

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,∠ABC、∠ACB 的角平分线交于点 O,MN 过点 O,且MN∥BC,分别交 AB、AC 于点 M、N.若 MN=5cm,CN=2cm,则 BM=________cm.
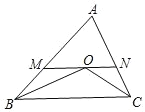
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
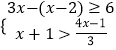 .并写出它的整数解.
.并写出它的整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段
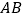 ,分别以
,分别以 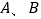 为圆心,大于
为圆心,大于  为半径作弧,连接弧的交点得到直线
为半径作弧,连接弧的交点得到直线 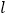 ,在直线
,在直线 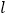 上取一点
上取一点  ,使得
,使得  ,延长
,延长 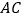 至
至 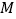 ,求
,求 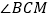 的度数为( )
的度数为( )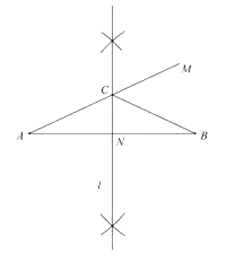
A.
B.
C.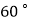
D.
相关试题

