【题目】如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴上,函数y=![]() 的图象过点P(4,3)和矩形的顶点B(m,n)(0<m<4).
的图象过点P(4,3)和矩形的顶点B(m,n)(0<m<4).

(1)求k的值;
(2)连接PA,PB,若△ABP的面积为6,求直线BP的解析式.
参考答案:
【答案】(1)k=12;(2)y=﹣![]() x+9
x+9
【解析】试题分析:把P(4,3)代入反比例函数解析式,即可求出k的值;由反比例函数的图象过点B(m,n),得出mn=12.根据△ABP的面积为6列出方程![]() n(4﹣m)=6,将mn=12代入,化简得4n﹣12=12,解方程求出n=6,再求出m=2,那么点B(2,6).设直线BP的解析式为y=ax+b,将B(2,6),P(4,3)代入,利用待定系数法即可求出直线BP的解析式.
n(4﹣m)=6,将mn=12代入,化简得4n﹣12=12,解方程求出n=6,再求出m=2,那么点B(2,6).设直线BP的解析式为y=ax+b,将B(2,6),P(4,3)代入,利用待定系数法即可求出直线BP的解析式.
试题解析:(1)∵函数y=![]() 的图象过点P(4,3),∴k=4×3=12;
的图象过点P(4,3),∴k=4×3=12;
(2)∵函数y=![]() 的图象过点B(m,n),[来∴mn=12. ∵△ABP的面积为6,P(4,3),0<m<4,
的图象过点B(m,n),[来∴mn=12. ∵△ABP的面积为6,P(4,3),0<m<4,
∴![]() n(4﹣m)=6,∴4n﹣12=12,解得n=6,∴m=2,∴点B(2,6).
n(4﹣m)=6,∴4n﹣12=12,解得n=6,∴m=2,∴点B(2,6).
设直线BP的解析式为y=ax+b,∵B(2,6),P(4,3),
∴![]() ,解得:
,解得:  ,∴直线BP的解析式为y=﹣
,∴直线BP的解析式为y=﹣![]() x+9.
x+9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数的图象与
 轴、
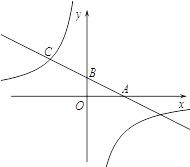
轴、 轴分别相交于A、B两点,且与反比例函数的图象在第二象限交于点C.如果点A的坐标为(4,0),OA=2OB,点 B是AC的中点.
轴分别相交于A、B两点,且与反比例函数的图象在第二象限交于点C.如果点A的坐标为(4,0),OA=2OB,点 B是AC的中点.(1)求点C的坐标;
(2)求一次函数和反比例函数的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某校开展了以“梦想中国”为主题的摄影大赛,要求参赛学生每人交一件作品.现将从中挑选的50件参赛作品的成绩(单位:分)统计如下:
等级
成绩(用m表示)
频数
频率
A
90≤m≤100
x
0.08
B
80≤m<90
34
y
C
m<80
12
0.24
合计
50
1
请根据上表提供的信息,解答下列问题:
(1)表中x的值为 , y的值为;(直接填写结果)
(2)将本次参赛作品获得A等级的学生依次用A1、A2、A3…表示.现该校决定从本次参赛作品获得A等级的学生中,随机抽取两名学生谈谈他们的参赛体会,则恰好抽到学生A1和A2的概率为 . (直接填写结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于
 BF长为半径画弧,两弧交于一点P,连
BF长为半径画弧,两弧交于一点P,连
接AP并延长交BC于点E,连接EF.
(1)四边形ABEF是;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为 , ∠ABC=°.(直接填写结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y1=kx+b(k≠0)的图象与反比例函数
 的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是﹣2.
的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是﹣2.(1)求一次函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出y1>y2时x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x+m(m>0)与x轴交于点A(-2,0),直线y=-x+n(n>0)与x轴、y轴分别交于B、C两点,并与直线y=2x+m(m>0)相交于点D,若AB=4.
(1)求点D的坐标;
(2)求出四边形AOCD的面积;
(3)若E为x轴上一点,且△ACE为等腰三角形,直接写出点E的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离y(km)与已用时间x(h)之间的关系,则小敏、小聪行走的速度分别是( )

A. 3km/h和4km/h B. 3km/h和3km/h
C. 4km/h和4km/h D. 4km/h和3km/h
相关试题

