搜索
【题目】小敏从A地出发向B地行走，同时小聪从B地出发向A地行走，如图所示，相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离y（km）与已用时间x（h）之间的关系，则小敏、小聪行走的速度分别是（ ）
A. 3km/h和4km/h B. 3km/h和3km/h
C. 4km/h和4km/h D. 4km/h和3km/h
参考答案：
【答案】D
【解析】设小敏的速度为：m，则函数式为，y=mx+b，
由已知小敏经过两点(1.6,4.8)和(2.8,0)，
所以得：4.8=1.6m+b，0=2.8m+b，
解得：m=4，b=11.2，
小敏离B地的距离y(km)与已用时间x(h)之间的关系为：y=4x+11.2；
由实际问题得小敏的速度为4km/h.
设小聪的速度为：n，则函数图象过原点则函数式为，y=nx，
由已知经过点(1.6,4.8)，
所以得：4.8=1.6n，
则n=3，
即小聪的速度为3km/h.
故选D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴，y轴上，函数y=
的图象过点P（4，3）和矩形的顶点B（m，n）（0＜m＜4）．
（1）求k的值；
（2）连接PA，PB，若△ABP的面积为6，求直线BP的解析式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知一次函数y1=kx+b（k≠0）的图象与反比例函数
的图象交于A、B两点，与坐标轴交于M、N两点．且点A的横坐标和点B的纵坐标都是﹣2．（1）求一次函数的解析式；
（2）求△AOB的面积；
（3）观察图象，直接写出y1＞y2时x的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=2x+m(m>0)与x轴交于点A(-2，0)，直线y=-x+n(n>0)与x轴、y轴分别交于B、C两点，并与直线y=2x+m(m>0)相交于点D，若AB=4．
（1）求点D的坐标；
（2）求出四边形AOCD的面积；
（3）若E为x轴上一点，且△ACE为等腰三角形，直接写出点E的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知在平面直角坐标系中，O是坐标原点，点A（2，5）在反比例函数y=
的图象上．一次函数y=x+b的图象过点A，且与反比例函数图象的另一交点为B．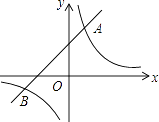
（1）求k和b的值；
（2）设反比例函数值为y1 ， 一次函数值为y2 ， 求y1＞y2时x的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，出租车是人们出行的一种便利交通工具，折线ABC是在我市乘出租车所付车费y（元）与行车里程x（km）之间的函数关系图象．
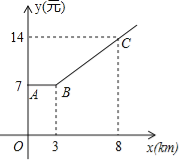
（1）根据图象，当x≥3时y为x的一次函数，请写出函数关系式；
（2）某人乘坐13km，应付多少钱？
（3）若某人付车费42元，出租车行驶了多少千米？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，点A坐标为(6，0)，点B在y轴的正半轴上，且
=240.(1)求点B坐标；
(2)若点P从B出发沿y轴负半轴方向运动，速度每秒2个单位，运动时间t秒，△AOP的面积为S，求S与t的关系式，并直接写出t的取值范围；
(3)在(2)的条件下，若S△AOP：S△ABP=1:3，且S△AOP+S△ABP=S△AOB，在线段AB的垂直平分线上是否存在点Q，使得△AOQ的面积与△BPQ的面积相等？若存在，求出Q点坐标；若不存在，请说明理由。
相关试题
