搜索
【题目】如图，已知点P是反比例函数y＝
(k1＜0，x＜0)图象上一点，过点P作x轴、y轴的垂线，分别交x轴、y轴于A、B两点，交反比例函数y＝
(0＜k2＜|k1|)图象于E、F两点．
（1）用含k1、k2的式子表示四边形PEOF的面积；
（2）若P点坐标为（－4，3），且PB：PF＝2：3，分别求出k1、k2的值．
参考答案：
【答案】(1) k2－k1；(2) k1＝－12 ，k2＝6．
【解析】试题分析：（1）这三个图形的面积运用反比例函数上的点的横纵坐标乘积等于反比例函数的系数的绝对值可解．①S四边形PAOB=|OA||OB|=|k1|；②S三角形OFB=
|BF||OB|=
；③S四边形PEOF=S四边形PAOB+S三角形OFB+S△EAO=k2﹣k1（或k2+|k1|）．
（2）由P（﹣4，3）在
上可得k1=﹣12，由PB：PF=2：3得BF=2，即F（2，3），故k2=6．
试题解析：解：（1）①S四边形PAOB=|OA||OB|=|k1|；
②S三角形OFB=
|BF||OB|=
；
③S四边形PEOF=S四边形PAOB+S三角形OFB+S△EAO=k2﹣k1（或k2+|k1|）；
（2）因为P（﹣4，3）在
上，∴k1=﹣12；
又PB：PF=2：3，∴F（2，3），∴k2=6．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ABC=50°，∠ACB=60°，点E在BC的延长线上，∠ABC的平分线BD与∠ACE的平分线CD相交于点D，连接AD，下列结论中不正确的是（ ）
A. ∠BAC=70° B. ∠DOC=90° C. ∠BDC=35° D. ∠DAC=55°
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个，小明做摸球试验，他将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是试验中的一组统计数据：
(1)请估计：当n很大时，摸到白球的概率约为______；(精确到0.1)
(2)估算盒子里有白球________个；
(3)若向盒子里再放入x个除颜色以外其他完全相同的球，这x个球中白球只有1个，每次将球搅拌均匀后，任意摸出一个球记下颜色再放回，通过大量重复摸球试验后发现，摸到白球的频率稳定在50%，请推测x的值最有可能是多少．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，把△ABC纸片沿DE折叠，当点A在四边形BCDE的外部时，记∠AEB为∠1，∠ADC为∠2，则∠A、∠1与∠2的数量关系，结论正确的是（ ）
A. ∠1＝∠2＋∠A B. ∠1＝2∠A＋∠2
C. ∠1＝2∠2＋2∠A D. 2∠1＝∠2＋∠A
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，Rt△ABO的顶点A是双曲线y＝
与直线y＝－x－(k＋1)在第二象限的交点．AB⊥x轴于B，且S△ABO＝
．(1)求这两个函数的解析式；
(2)求直线与双曲线的两个交点A．C的坐标和△AOC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知反比例函数y＝
（k1＞0）与一次函数y＝k2x＋1（k2≠0）的图象交于A，B两点，AC⊥x轴于点C．若△OAC的面积为1，且AC＝2OC．
（1）求反比例函数与一次函数的解析式；
（2）请直接写出点B的坐标；
（3）当x为何值时，反比例函数的值大于一次函数的值？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，面积为8的矩形ABOC的边OB、OC分别在x轴、y轴的正半轴上，点A在双曲线y＝
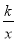的图象上，且AC＝2．（1）求k值；
（2）矩形BDEF，BD在x轴的正半轴上，F在AB上，且BD＝OC，BF＝OB．双曲线交DE于M点，交EF于N点，求△MEN的面积．
相关试题
