【题目】如图,面积为8的矩形ABOC的边OB、OC分别在x轴、y轴的正半轴上,点A在双曲线y=![]() 的图象上,且AC=2.
的图象上,且AC=2.
(1)求k值;
(2)矩形BDEF,BD在x轴的正半轴上,F在AB上,且BD=OC,BF=OB.双曲线交DE于M点,交EF于N点,求△MEN的面积.

参考答案:
【答案】(1)y=![]() ;(2)
;(2) ![]()
【解析】试题分析:(1)根据矩形的面积求出AB,求出A的坐标,代入反比例函数解析式求出即可;
(2)先求出BF和OD,代入函数解析式求出点的坐标,求出EN和EM,根据面积公式求出即可.
试题解析:解:(1)∵矩形ABOC的面积为8,AC=2,∴OC=AB=8÷2=4,AC=OB=2,∴A点的坐标为(2,4),∵点A在双曲线![]() 的图象上,∴代入得:k=8;
的图象上,∴代入得:k=8;
(2)由(1)知:反比例函数的解析式为![]() ,∵BD=OC,BF=OB,OC=4,OB=2,又∵四边形BDEF是矩形,∴BD=EF=4,BF=DE=2,OD=BD+OB=6,把y=2代入
,∵BD=OC,BF=OB,OC=4,OB=2,又∵四边形BDEF是矩形,∴BD=EF=4,BF=DE=2,OD=BD+OB=6,把y=2代入![]() 得:x=4,即N点的坐标为(4,2),把x=6代入
得:x=4,即N点的坐标为(4,2),把x=6代入![]() 得:y=
得:y=![]() ,即M的坐标为(6,
,即M的坐标为(6, ![]() ),∴EN=6﹣4=2,EM=2﹣
),∴EN=6﹣4=2,EM=2﹣![]() =
=![]() ,∴△MEN的面积为
,∴△MEN的面积为![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点P是反比例函数y=
 (k1<0,x<0)图象上一点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交反比例函数y=
(k1<0,x<0)图象上一点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交反比例函数y= (0<k2<|k1|)图象于E、F两点.
(0<k2<|k1|)图象于E、F两点.(1)用含k1、k2的式子表示四边形PEOF的面积;
(2)若P点坐标为(-4,3),且PB:PF=2:3,分别求出k1、k2的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABO的顶点A是双曲线y=
 与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO= .
.(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A.C的坐标和△AOC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y=
 (k1>0)与一次函数y=k2x+1(k2≠0)的图象交于A,B
(k1>0)与一次函数y=k2x+1(k2≠0)的图象交于A,B两点,AC⊥x轴于点C.若△OAC的面积为1,且AC=2OC.
(1)求反比例函数与一次函数的解析式;
(2)请直接写出点B的坐标;
(3)当x为何值时,反比例函数的值大于一次函数的值?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
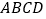 中,
中,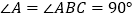 ,
,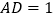 ,
,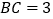 ,
,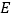 是边
是边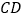 的中点,连接
的中点,连接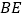 延长与
延长与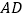 的延长线相交于点
的延长线相交于点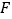 ,连接
,连接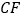 .
.(
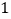 )求证:四边形
)求证:四边形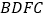 是平行四边形.
是平行四边形.(
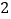 )已知
)已知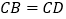 ,求四边形
,求四边形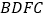 的面积.
的面积.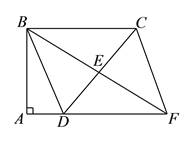
-
科目: 来源: 题型:
查看答案和解析>>【题目】在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )

A. 两人都对 B. 两人都不对 C. 甲对,乙不对 D. 甲不对,乙对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y1=
 与正比例函数y2=k2x相交于点A(-1,-3)和点B.
与正比例函数y2=k2x相交于点A(-1,-3)和点B.(1)求k1,k2的值;
(2)写出点B的坐标;
(3)写出
 >k2x的解集.
>k2x的解集.
相关试题

