【题目】为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,从该地区随机抽取部分七年级学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名同学只能选择其中一类节目),并调查得到的数据用下面的表和扇形图来表示(表、图都没制作完成)

根据表、图提供的信息,解决以下问题:
(1)计算出表中a、b的值;
(2)求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数;

(3)若该地区七年级学生共有47500人,试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人?
参考答案:
【答案】(1)162,135;(2)108°;(3)3800.
【解析】
试题分析:(1)先求出抽取的总人数,再求出b的值,进而可得出a的值;
(2)求出a的值与总人数的比可得出结论;
(3)求出喜爱新闻类人数的百分比,进而可得出结论.
试题解析:(1)∵喜欢体育的人数是90人,占总人数的20%,∴总人数=![]() =450(人).
=450(人).
∵娱乐人数占36%,∴a=450×36%=162(人),∴b=450﹣162﹣36﹣90﹣27=135(人);
(2)∵喜欢动画的人数是135人,∴![]() ×360°=108°;
×360°=108°;
(3)∵喜爱新闻类人数的百分比=![]() ×100%=8%,∴47500×8%=3800(人).
×100%=8%,∴47500×8%=3800(人).
答:该地区七年级学生中喜爱“新闻”类电视节目的学生有3800人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=x2+6x+8,使函数值y>0的x的取值范围是( )
A. x<-4且x>-2 B. x<-4或x>-2 C. -4<x<-2 D. x<-4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果水位升高3m时水位变化记作+3m,那么水位下降3m时水位变化记作 ( )
A. -3m B. 3 m C. 6 m D. -6 m
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角三角形ABC中,∠ACB=90°,∠A=33°,将三角形ABC沿AB方向向右平移得到三角形DEF.
(1)试求出∠E的度数;
(2)若AE=9 cm,DB=2 cm,求出BE的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(
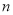 ,
, 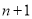 ),B(
),B(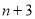 ,
, 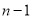 )是反比例函数
)是反比例函数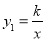 (x>0)的图像与一次函数
(x>0)的图像与一次函数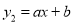 图像的两个交点.求:
图像的两个交点.求:(1)反比例函数与一次函数的表达式;
(2)根据图像直接写出当
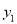 >
>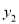 时x的取值范围;
时x的取值范围;(3)P是反比例函数
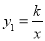 (x>0)图像上A、B之间的一点,AC⊥y轴于点C,BD⊥x轴于点D,若△PAC和△PBD的面积相等,求点P的坐标.
(x>0)图像上A、B之间的一点,AC⊥y轴于点C,BD⊥x轴于点D,若△PAC和△PBD的面积相等,求点P的坐标.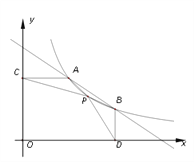
-
科目: 来源: 题型:
查看答案和解析>>【题目】请把下列的证明过程补充完整:
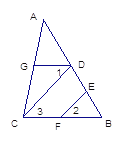
如图,已知∠AGD=∠ACB,∠1=∠2。求证:CD∥EF。(填空并在后面的括号中填理由)
证明:∵∠AGD=∠ACB( )
∴DG∥ ( )
∴∠3= ( )
∵∠1=∠2 ( )
∴∠3= (等量代换)
∴ ∥ ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b(k<0)与反比例函数
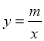 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)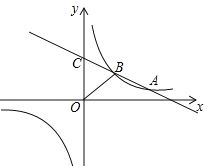
(1)求反比例函数的解析式;
(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.
相关试题

