【题目】如图,一次函数y=kx+b(k<0)与反比例函数![]() 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
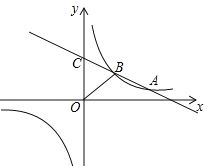
(1)求反比例函数的解析式;
(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)由点A的坐标结合反比例函数系数k的几何意义,即可求出m的值;
(2)设点B的坐标为(n,![]() ),将一次函数解析式代入反比例函数解析式中,利用根与系数的关系可找出n、k的关系,由三角形的面积公式可表示出来b、n的关系,再由点A在一次函数图象上,可找出k、b的关系,联立3个等式为方程组,解方程组即可得出结论.
),将一次函数解析式代入反比例函数解析式中,利用根与系数的关系可找出n、k的关系,由三角形的面积公式可表示出来b、n的关系,再由点A在一次函数图象上,可找出k、b的关系,联立3个等式为方程组,解方程组即可得出结论.
试题解析:(1)∵点A(4,1)在反比例函数![]() 的图象上,∴m=4×1=4,∴反比例函数的解析式为
的图象上,∴m=4×1=4,∴反比例函数的解析式为![]() .
.
(2)∵点B在反比例函数![]() 的图象上,∴设点B的坐标为(n,
的图象上,∴设点B的坐标为(n,![]() ).
).
将y=kx+b代入![]() 中,得:
中,得:
kx+b=![]() ,整理得:
,整理得:![]() ,∴4n=
,∴4n=![]() ,即nk=﹣1①.
,即nk=﹣1①.
令y=kx+b中x=0,则y=b,即点C的坐标为(0,b),∴S△BOC=![]() bn=3,∴bn=6②.
bn=3,∴bn=6②.
∵点A(4,1)在一次函数y=kx+b的图象上,∴1=4k+b③.
联立①②③成方程组,即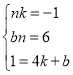 ,解得:
,解得: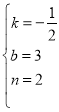 ,∴该一次函数的解析式为
,∴该一次函数的解析式为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,从该地区随机抽取部分七年级学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名同学只能选择其中一类节目),并调查得到的数据用下面的表和扇形图来表示(表、图都没制作完成)

根据表、图提供的信息,解决以下问题:
(1)计算出表中a、b的值;
(2)求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数;

(3)若该地区七年级学生共有47500人,试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(
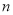 ,
, 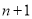 ),B(
),B(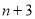 ,
, 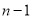 )是反比例函数
)是反比例函数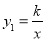 (x>0)的图像与一次函数
(x>0)的图像与一次函数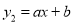 图像的两个交点.求:
图像的两个交点.求:(1)反比例函数与一次函数的表达式;
(2)根据图像直接写出当
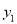 >
>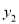 时x的取值范围;
时x的取值范围;(3)P是反比例函数
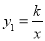 (x>0)图像上A、B之间的一点,AC⊥y轴于点C,BD⊥x轴于点D,若△PAC和△PBD的面积相等,求点P的坐标.
(x>0)图像上A、B之间的一点,AC⊥y轴于点C,BD⊥x轴于点D,若△PAC和△PBD的面积相等,求点P的坐标.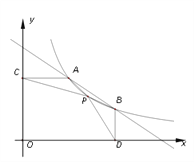
-
科目: 来源: 题型:
查看答案和解析>>【题目】请把下列的证明过程补充完整:
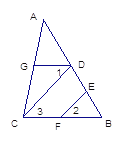
如图,已知∠AGD=∠ACB,∠1=∠2。求证:CD∥EF。(填空并在后面的括号中填理由)
证明:∵∠AGD=∠ACB( )
∴DG∥ ( )
∴∠3= ( )
∵∠1=∠2 ( )
∴∠3= (等量代换)
∴ ∥ ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价
成本价
销售价(元/箱)
甲
24
36
乙
33
48
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=(x-1)2+3向左平移1个单位,再向下平移3个单位所得抛物线的解析式为( )
A. y=x2 B. y=(x-2)2+6 C. y=x2+6 D. y=(x-2)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形的每一个外角都是40°,则这个多边形的内角的度数是( )
A. 1080° B. 1440° C. 1260° D. 1080°
相关试题

