【题目】已知实数![]() +1的整数部分为m,小数部分为n.
+1的整数部分为m,小数部分为n.
(1)求m,n的值;
(2)在平面直角坐标系中,试判断点(m﹣1,n﹣1)位于第几象限;
(3)若m,n+1为一个直角三角形的斜边与一条直角边的长,求这个直角三角形的面积.
参考答案:
【答案】(1)m=2,n=![]() ;(2)第四象限;(3)
;(2)第四象限;(3)![]() .
.
【解析】
(1)根据无理数的估计解答即可;(2)根据平面直角坐标系中象限的特点解答即可;(3)根据勾股定理求得直角三角形另一条直角边的长,再利用三角形的面积公式求解即可.
(1)∵![]() ,
,
∴![]() ,
,
∴m=2,n=![]() =
=![]() ;
;
(2)∵m-1=2-1>0,n-1=![]() -1=
-1=![]() <0,
<0,
∴点(m﹣1,n﹣1)位于第四象限;
(3)由题意可知,直角三角形的斜边长为2,一条直角边长为![]() ,
,
由勾股定理可得另一条直角边为1,
∴直角三角形的面积为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直角坐标系中,函数y=kx2﹣k和y=kx+k(k≠0)的图象大致是( )
A.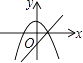
B.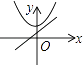
C.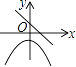
D.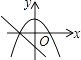
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系中,点P从原点O以每秒1个单位速度沿x轴正方向运动,运动时间为t秒,作点P关于直线y=tx的对称点Q,过点Q作x轴的垂线,垂足为点A.
(1)当t=2时,求AO的长.
(2)当t=3时,求AQ的长.
(3)在点P的运动过程中,用含t的代数式表示线段AP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,(M2,N2),∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD,CD.
(1)求证:△ADE≌△CDB;
(2)若BC=
 ,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.
,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,△ABC的边BC在x轴上,A,C两点的坐标分别为A(0,m),C(n,0),B(﹣5,0),且(n﹣3)2+
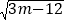 =0.一动点P从点B出发,以每秒2单位长度的速度沿射线BO匀速运动,设点P运动的时间为ts.
=0.一动点P从点B出发,以每秒2单位长度的速度沿射线BO匀速运动,设点P运动的时间为ts.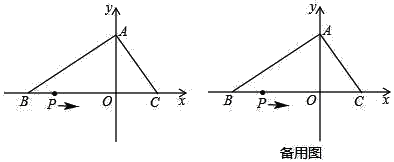
(1)求A,C两点的坐标;
(2)连接PA,若△PAB为等腰三角形,求点P的坐标;
(3)当点P在线段BO上运动时,在y轴上是否存在点Q,使△POQ与△AOC全等?若存在,请求出t的值并直接写出点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )

A. 20 B. 25 C. 30 D. 32
-
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积进行了证明.著名数学家华罗庚提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.
请根据图1中直角三角形叙述勾股定理.

以图1中的直角三角形为基础,可以构造出以a,b为底,以a+b为高的直角梯形(如图2).请你利用图2,验证勾股定理;
利用图2中的直角梯形,我们可以证明
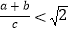 .其证明步骤如下:
.其证明步骤如下:∵BC=a+b,AD=_____;
又∵在直角梯形ABCD中有BC_____AD(填大小关系),即_____.
∴
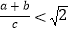 .
.
相关试题

