【题目】如图,已知在平面直角坐标系中,点P从原点O以每秒1个单位速度沿x轴正方向运动,运动时间为t秒,作点P关于直线y=tx的对称点Q,过点Q作x轴的垂线,垂足为点A.
(1)当t=2时,求AO的长.
(2)当t=3时,求AQ的长.
(3)在点P的运动过程中,用含t的代数式表示线段AP的长.

参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() .
.
【解析】
过P作PD⊥x轴,交直线y=tx于D,连接OQ,
(1)证△OPD∽△QAP,得![]() ,AP=2AQ,设AQ=a,
,AP=2AQ,设AQ=a,
由勾股定理得:OQ2=AQ2+AO2,![]() ;
;
②设AQ=a,Rt△AQO中,由勾股定理得:OQ2=AQ2+AO2,![]() ;
;
(3)同理OP=t,PD=t2,△OPD∽△QAP,故![]() ,AP=tAQ,在Rt△AQO中,OQ=OP=t,由勾股定理得:OQ2=AQ2+AO2,
,AP=tAQ,在Rt△AQO中,OQ=OP=t,由勾股定理得:OQ2=AQ2+AO2,![]() .
.
解:过P作PD⊥x轴,交直线y=tx于D,连接OQ,
(1)当t=2时,y=PD=2x=4,
∵∠BDP+∠DPB=∠DPB+∠APQ=90°,
∴∠BDP=∠APQ,
∴△OPD∽△QAP,
∴![]() ,
,
∴AP=2AQ,
设AQ=a,
Rt△AQO中,OQ=OP=2,
由勾股定理得:OQ2=AQ2+AO2,
∴![]() ,
,
5a2+4a﹣12=0,
a1=﹣2(舍),a2=![]() ,
,
∴AO=![]() ;
;
②当t=3时,OP=3,PD=9,
设AQ=a,
Rt△AQO中,OQ=OP=3,
由勾股定理得:OQ2=AQ2+AO2,
![]() ,
,
5a2+3a﹣36=0,
(a+3)(5a﹣12)=0,
a1=﹣3(舍),a2=![]() ,
,
∴AQ=![]() AP=
AP=![]() (
(![]() +3)=
+3)=![]() ;
;
(3)同理OP=t,PD=t2,
∴△OPD∽△QAP,
∴![]() ,
,
∴AP=tAQ,
Rt△AQO中,OQ=OP=t,
由勾股定理得:OQ2=AQ2+AO2,
∴![]() ,
,
AP=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,AH⊥BC,垂足为点H,若AB+BH=CH,∠ABH=70°,则∠BAC=_____°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABO中,AB⊥OB,OB=
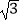 ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1坐标为( )
,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1坐标为( ) 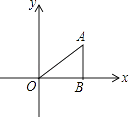
A.(﹣1,﹣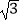 )
)
B.(﹣1,﹣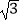 )或(﹣2,0)
)或(﹣2,0)
C.(﹣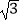 ,1)或(0,﹣2)
,1)或(0,﹣2)
D.(﹣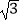 ,1)
,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直角坐标系中,函数y=kx2﹣k和y=kx+k(k≠0)的图象大致是( )
A.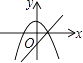
B.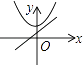
C.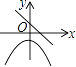
D.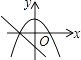
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,(M2,N2),∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD,CD.
(1)求证:△ADE≌△CDB;
(2)若BC=
 ,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.
,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数
 +1的整数部分为m,小数部分为n.
+1的整数部分为m,小数部分为n.(1)求m,n的值;
(2)在平面直角坐标系中,试判断点(m﹣1,n﹣1)位于第几象限;
(3)若m,n+1为一个直角三角形的斜边与一条直角边的长,求这个直角三角形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,△ABC的边BC在x轴上,A,C两点的坐标分别为A(0,m),C(n,0),B(﹣5,0),且(n﹣3)2+
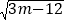 =0.一动点P从点B出发,以每秒2单位长度的速度沿射线BO匀速运动,设点P运动的时间为ts.
=0.一动点P从点B出发,以每秒2单位长度的速度沿射线BO匀速运动,设点P运动的时间为ts.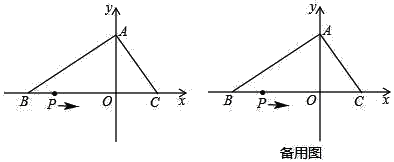
(1)求A,C两点的坐标;
(2)连接PA,若△PAB为等腰三角形,求点P的坐标;
(3)当点P在线段BO上运动时,在y轴上是否存在点Q,使△POQ与△AOC全等?若存在,请求出t的值并直接写出点Q的坐标;若不存在,请说明理由.
相关试题

