【题目】如图,△ ![]() 内接于⊙O,过点B作⊙O的切线DE,F为射线BD上一点,连接CF
内接于⊙O,过点B作⊙O的切线DE,F为射线BD上一点,连接CF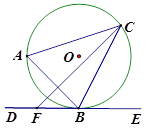
(1)求证: ![]() ;
;
(2)若⊙O 的直径为5, ![]() ,
, ![]() ,求
,求 ![]() 的长.
的长.
参考答案:
【答案】
(1)证明:
如图:连接BO并延长交⊙O于点M,连接MC.

∴∠A=∠M,∠MCB=90°.
∴∠M+∠MBC=90°.
∵DE是⊙O的切线,
∴∠CBE+∠MBC=90°.
∴ ![]() .
.
∴ ![]() .
.
(2)解:过点 ![]() 作
作 ![]() 于点
于点 ![]() .
.
∴ ![]() .
.
由(1)得, ![]() .
.
∴ ![]() .
.
在Rt△ ![]() 中,
中,
∵ ![]() ,
,
∴ ![]() .
.
在Rt△ ![]() 中,
中,
∵ ![]() ,
,
∴ ![]() .
.
∵ ![]() ,
,
∴ ![]() .
.
在Rt△ ![]() 中,
中,
∵ ![]() ,
,
∴ ![]() .
.
【解析】(1)根据圆周角定理和直径的性质,得到∠M+∠MBC=90°,再由DE是⊙O的切线,根据切线的性质,得到∠CBE=∠A;(2)由(1)得,∠M=∠CBE=∠A ,由tanA=2,根据三角函数得到tanM=tan∠CBE= tanA,根据勾股定理求出BC的值,求出CF的值.
【考点精析】本题主要考查了切线的性质定理和同角三角函数的关系(倒数、平方和商)的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;各锐角三角函数之间的关系:平方关系(sin2A+cos2A=1);倒数关系(tanAtan(90°—A)=1);弦切关系(tanA=sinA/cosA )才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,CD=1.5,BD=2.5,求AC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
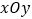 中,双曲线
中,双曲线 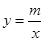 与直线
与直线 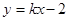 交于点A(3,1).
交于点A(3,1).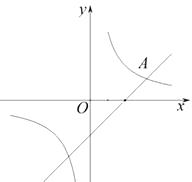
(1)求直线和双曲线的解析式;
(2)直线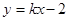 与x轴交于点B,点P是双曲线
与x轴交于点B,点P是双曲线 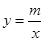 上一点,过点P作直线PC∥x轴,交y轴于点C,交直线
上一点,过点P作直线PC∥x轴,交y轴于点C,交直线 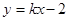 于点D.若DC=2OB,直接写出点
于点D.若DC=2OB,直接写出点 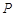 的坐标为 .
的坐标为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的
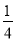 ?若存在求出此时点M的坐标;若不存在,说明理由.
?若存在求出此时点M的坐标;若不存在,说明理由.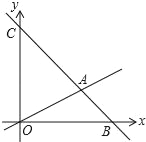
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了保护环境,某化工厂一期工程完成后购买了3台甲型和2台乙型污水处理设备,共花费资金54万元,且每台乙型设备的价格是每台甲型设备价格的75%.
(1)请你计算每台甲型设备和每台乙型设备的价格各是多少元?
(2)今年该厂二期工程即将完成,产生的污水将大大增加,于是该厂决定再购买甲、乙两种型号设备共8台用于二期工程的污水处理,预算本次购买资金不超过84万元;实际运行中发现,每台甲型设备每月能处理污水200吨,每台乙型设备每月能处理污水160吨,预计二期工程完成后每月将产生不少于1300吨污水,请你求出用于二期工程的污水处理设备的所有购买方案.
(3)经测算:每年用于每台甲型设备的各种维护费和电费为1万元,每年用于每台乙型设备的各种维护费和电费为1.5万元.在(2)中的方案中,哪种购买方案使得设备的各种维护费和电费总费用最低?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,下列推理及括号中所注明的推理依据错误的是( ).
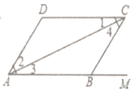
A.∵
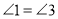 ,∴
,∴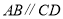 (内错角相等,两直线平行)
(内错角相等,两直线平行)B.∵
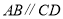 ,∴
,∴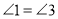 (两直线平行,内错角相等)
(两直线平行,内错角相等)C.∵
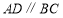 ,∴
,∴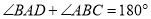 (两直线平行,同旁内角互补)
(两直线平行,同旁内角互补)D.∵
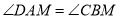 ,∴
,∴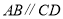 (同位角相等,两直线平行)
(同位角相等,两直线平行) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
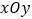 中,定义直线
中,定义直线 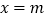 与双曲线
与双曲线 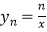 的交点
的交点 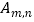 (m、n为正整数)为 “双曲格点”,双曲线
(m、n为正整数)为 “双曲格点”,双曲线 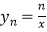 在第一象限内的部分沿着竖直方向平移或以平行于
在第一象限内的部分沿着竖直方向平移或以平行于 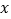 轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.
轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.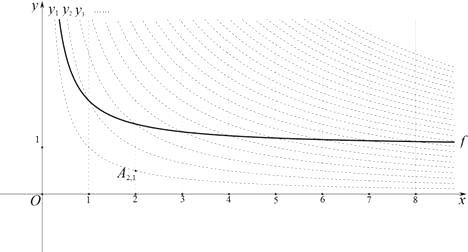
(1)①“双曲格点”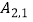 的坐标为;
的坐标为;
②若线段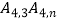 的长为1个单位长度,则n=;
的长为1个单位长度,则n=;
(2)图中的曲线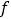 是双曲线
是双曲线 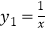 的一条“派生曲线”,且经过点
的一条“派生曲线”,且经过点 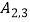 ,则
,则 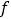 的解析式为 y=;
的解析式为 y=;
(3)画出双曲线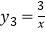 的“派生曲线”g(g与双曲线
的“派生曲线”g(g与双曲线 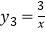 不重合),使其经过“双曲格点”
不重合),使其经过“双曲格点” 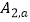 、
、 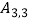 、
、 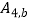 .
.
相关试题

