【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() ,
,![]() 轴分别相交于点
轴分别相交于点![]() 、
、![]() ,与直线
,与直线![]() 交于点
交于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
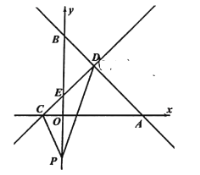
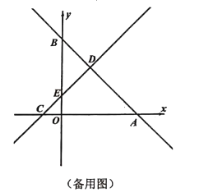
(1)若点![]() 是
是![]() 轴上一动点,连接
轴上一动点,连接![]() 、
、![]() ,求当
,求当![]() 取最大值时,
取最大值时,![]() 点的坐标;
点的坐标;
(2)在(1)问的条件下,将![]() 沿
沿![]() 轴平移,在平移的过程中,直线
轴平移,在平移的过程中,直线![]() 交直线
交直线![]() 于点
于点![]() ,则当
,则当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长.
的长.
参考答案:
【答案】(1)P点坐标为![]() ;(2)BM的长为
;(2)BM的长为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)将D点坐标代入![]() 求出m的值,然后求出C点坐标,作C点关于y轴的对称点C',连接DC',与y轴的交点即为点P,求出DC'直线解析式,即可求出P点坐标;
求出m的值,然后求出C点坐标,作C点关于y轴的对称点C',连接DC',与y轴的交点即为点P,求出DC'直线解析式,即可求出P点坐标;
(2)将![]() 代入直线
代入直线![]() ,求出b的值,再求A点坐标,设M点坐标为
,求出b的值,再求A点坐标,设M点坐标为![]() ,分三种情况讨论:①PA=PM,②PM=AM,③PA=AM,分别求出BM的长即可.
,分三种情况讨论:①PA=PM,②PM=AM,③PA=AM,分别求出BM的长即可.
(1)将![]() 代入
代入![]() 得:
得:![]()
∴![]()
当y=0时,![]() ,解得
,解得![]()
∴![]()
则![]() 关于y轴的对称点
关于y轴的对称点![]()
∴PC=PC',![]()
当P,C',D共线时,![]() 取得的最大值,如图所示,
取得的最大值,如图所示,
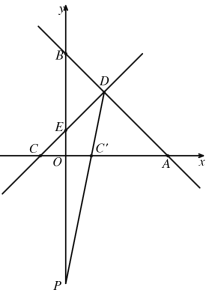
设直线PD解析式为![]() ,
,
将![]() ,
,![]() 代入得:
代入得:![]()
解得![]()
∴直线PD解析式为![]()
当x=0时,![]() ,
,
∴P点坐标为![]()
(2)将![]() 代入直线
代入直线![]() 得:
得:![]() ,
,
解得![]()
∴直线AB解析式为![]()
当y=0时,![]() ,解得
,解得![]() ,当x=0时,y=8
,当x=0时,y=8
∴A点坐标为![]() ,B点坐标为
,B点坐标为![]()
设M点坐标为![]()
①当PA=PM时,如图所示,
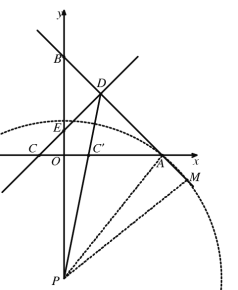
则![]()
解得![]() 或
或![]() (舍去)
(舍去)
此时M![]()
BM=![]()
②当PM=AM时,
则![]()
解得![]()
此时![]()
BM=![]()
③当PA=AM时,如图所示,
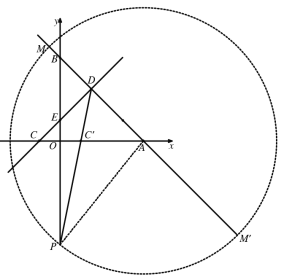
∵AB=![]() ,AM=AM'=PA=
,AM=AM'=PA=![]()
∴BM=AM-AB=![]() ,BM'=AM'+AB=
,BM'=AM'+AB=![]()
综上可得,BM的长为![]() 或
或![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究题
问题背景:如图1,在
 中,
中, 、
、 、
、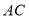 三边的长分别为
三边的长分别为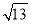 ,
, ,
,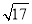 ,求
,求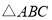 的面积.
的面积.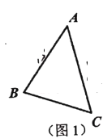
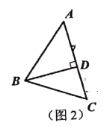
(1)问题解决:小明在计算这个三角形面积的时候,采用了传统的三角形面积计算公式的方法计算,即求出三角形的一条高.如图2,他过点
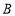 作
作 于点
于点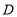 ,为了求出高
,为了求出高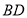 的长,他设
的长,他设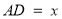 ,则
,则 ,根据勾股定理,可列方程:_______________________,该方程解得
,根据勾股定理,可列方程:_______________________,该方程解得 __________,再根据股定理求出高
__________,再根据股定理求出高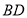 的长,从而计算
的长,从而计算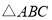 的面积(注:此小问不用计算
的面积(注:此小问不用计算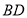 的长和
的长和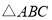 的面积);
的面积);(2)思维拓展:小辉同学在思考这个问题时,觉得小明的方法在计算上比较复杂,他先建立了一个正方形网格(每个正方形网格的边长是1),再在网格中画出了格点
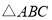 (即
(即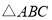 的三个顶点都在正方形的网格线的交点处),如图3,这样就不用求
的三个顶点都在正方形的网格线的交点处),如图3,这样就不用求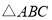 的高,直接借助网格就能计算
的高,直接借助网格就能计算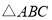 的面积为__________(直接写出
的面积为__________(直接写出 的面积即可);
的面积即可);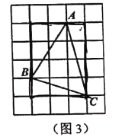


(3)方法应用:我们将小辉的方法称为“构图法”,若
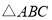 的三边长分别为
的三边长分别为 ,
,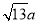 ,
, (
(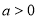 ),请在图4的网格中(网格中每个小正方形的边长为
),请在图4的网格中(网格中每个小正方形的边长为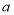 )画出相应的
)画出相应的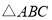 ,并求出它的面积;
,并求出它的面积;(4)探索创新:若
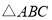 中有两边长为
中有两边长为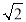 ,
, ,且
,且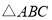 的面积为2,请在图5和备用图的正方形网格中画出
的面积为2,请在图5和备用图的正方形网格中画出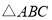 所有可能情况(全等三角形视为同一种情况),则
所有可能情况(全等三角形视为同一种情况),则 的第三边长为______________(直接写出所有可能的情况).
的第三边长为______________(直接写出所有可能的情况). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点G,连接AG交BE于点H,连接DH,下列结论正确的个数是( )
①△ABG∽△FDG ②HD平分∠EHG ③AG⊥BE ④S△HDG:S△HBG=tan∠DAG ⑤线段DH的最小值是2
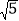 ﹣2.
﹣2.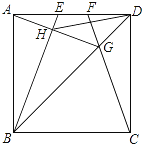
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣4x+4与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,将正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线在第一象限的分支上,则a的值是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角△ABC中,AC=BC,BE平分∠ABC,AD⊥BE的延长线于点D,若AD=2,则△ABE的面积为( ).
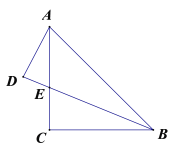
A.4B.6C.2
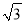 D.2
D.2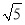
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知长方形纸片ABCD中,AB=10,AD=8,点E在AD边上,将△ABE沿BE折叠后,点A正好落在CD边上的点F处.
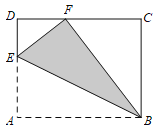
(1)求DF的长;
(2)求△BEF的面积.
相关试题

