【题目】如图,等腰直角△ABC中,AC=BC,BE平分∠ABC,AD⊥BE的延长线于点D,若AD=2,则△ABE的面积为( ).
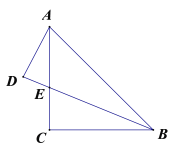
A.4B.6C.2![]() D.2
D.2![]()
参考答案:
【答案】A
【解析】
过点E作![]() 于F,设
于F,设![]() ,运用等腰直角三角形将其它各未知线段用
,运用等腰直角三角形将其它各未知线段用![]() 表示;延长AD与BC的延长线交于点G,依据ASA判定△ABD≌△GBD,依据全等的性质求得DG=AD=2,
表示;延长AD与BC的延长线交于点G,依据ASA判定△ABD≌△GBD,依据全等的性质求得DG=AD=2,![]() ,继而得到AG=4,
,继而得到AG=4,![]() ;接着在直角△ACG中,运用勾股定理列出关于的方程,解出代入到
;接着在直角△ACG中,运用勾股定理列出关于的方程,解出代入到![]() 中即可.
中即可.
解:延长AD与BC的延长线交于点G,过点E作![]() 于F,
于F,

易得![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]()
∵BE平分∠ABC,EC⊥BC,![]() ,
,
∴EF=EC,![]() ,
,
∴![]()
设![]()
则![]() ,
,![]() ,
,
∵AD⊥BE,
∴![]() ,
,
∵在△ABD和△GBD中,
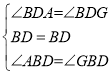
∴△ABD≌△GBD(ASA)
∴DG=AD=2,![]()
∴AG=4, ![]()
∵在直角△ACG中,![]() ACG=90°,
ACG=90°,![]() ,AG=4,
,AG=4,![]() ,
,
∴![]()
∴![]()
∴![]() =4.
=4.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点G,连接AG交BE于点H,连接DH,下列结论正确的个数是( )
①△ABG∽△FDG ②HD平分∠EHG ③AG⊥BE ④S△HDG:S△HBG=tan∠DAG ⑤线段DH的最小值是2
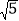 ﹣2.
﹣2.
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
 与
与 ,
,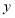 轴分别相交于点
轴分别相交于点 、
、 ,与直线
,与直线 交于点
交于点 ,直线
,直线 交
交 轴于点
轴于点 ,交
,交 轴于点
轴于点 .
.
(1)若点
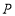 是
是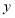 轴上一动点,连接
轴上一动点,连接 、
、 ,求当
,求当 取最大值时,
取最大值时,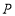 点的坐标;
点的坐标;(2)在(1)问的条件下,将
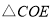 沿
沿 轴平移,在平移的过程中,直线
轴平移,在平移的过程中,直线 交直线
交直线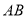 于点
于点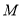 ,则当
,则当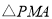 是等腰三角形时,求
是等腰三角形时,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣4x+4与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,将正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线在第一象限的分支上,则a的值是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知长方形纸片ABCD中,AB=10,AD=8,点E在AD边上,将△ABE沿BE折叠后,点A正好落在CD边上的点F处.
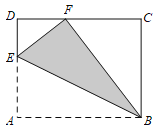
(1)求DF的长;
(2)求△BEF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),在建立的平面直角坐标系中,△ABC绕旋转中心P逆时针旋转90°后得到△A1B1C1.
(1)在图中标示出旋转中心P,并写出它的坐标;
(2)以原点O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2,在图中画出△A2B2C2,并写出C2的坐标.
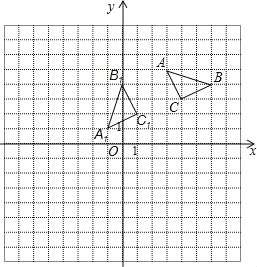
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个三角形的所有顶点都在网格的格点上,那么这个三角形叫做格点三角形,请在下列给定网格中按要求解答下面问题:
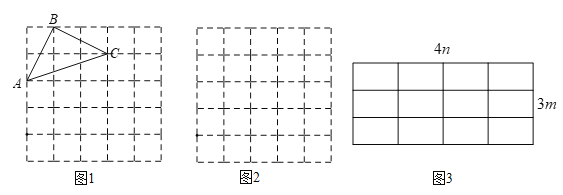
(1)直接写出图1方格图(每个小方格边长均为1)中格点△ABC的面积;
(2)已知△A1B1C1三边长分别为
 、
、 、
、 ,在图2方格图(每个小方格边长均为1)中画出格点△A1B1C1;
,在图2方格图(每个小方格边长均为1)中画出格点△A1B1C1;(3)已知△A2B2C2三边长分别为
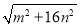 、
、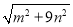 、
、  (m>0,n>0,且m≠n)在图3所示4n×3m网格中画出格点△A2B2C2,并求其面积.
(m>0,n>0,且m≠n)在图3所示4n×3m网格中画出格点△A2B2C2,并求其面积.
相关试题

