【题目】如图,在△ABC 中,∠BAC=120°,点 D 是 BC 上一点,BD 的垂直平分线交 AB 于点E,将△ACD 沿 AD 折叠,点 C 恰好与点 E 重合,则∠B 等于_______°;

参考答案:
【答案】20
【解析】
根据折叠的性质得出∠C=∠AED,再利用线段垂直平分线的性质得出BE=DE,进而得出∠B=∠EDB,进而得出∠C=2∠B,利用三角形内角和解答即可.
∵将△ACD沿AD折叠,点C恰好与点E重合,
∴∠C=∠AED,
∵BD的垂直平分线交AB于点E,
∴BE=DE,
∴∠B=∠EDB,
∴∠C=∠AED=∠B+∠EDB=2∠B,
在△ABC中,∠B+∠C+∠BAC=∠B+2∠B+120°=180°,
解得:∠B=20°,
故答案为20
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程
 -(k+2)x+2k=0.
-(k+2)x+2k=0.(1)试说明无论k取何值时,这个方程一定有实数根;
(2)已知等腰
 的一边a=1,若另两边b、c恰好是这个方程的两个根,求
的一边a=1,若另两边b、c恰好是这个方程的两个根,求 的周长.
的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知 AD 为△ABC 的高线,AD=BC,以 AB 为底边作等腰 Rt△ABE,连接 ED, EC,延长CE 交AD 于F 点,下列结论:①△ADE≌△BCE;②CE⊥DE;③BD=AF;④S△BDE=S△ACE,其中正确的有( )

A. ①③B. ①②④C. ①②③④D. ②③④
-
科目: 来源: 题型:
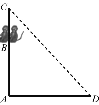
查看答案和解析>>【题目】如图所示,AC是一根垂直于地面的木杆,B是木杆上的一点,且AB=2米,D是地面上一点,AD=3米.在B处有甲、乙两只猴子,D处有一堆食物.甲猴由B往下爬到A处再从地面直奔D处,乙猴则向上爬到木杆顶C处腾空直扑到D处,如果两猴所经过的距离相等,则木杆的长为( )
A.
 m B. 2
m B. 2 m C. 3
m C. 3 m D. 5 m
m D. 5 m -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC 为等边三角形,点 D、E 分别在边 BC、AC 上,且 AE=CD,AD 与 BE相交于点 F.则∠DFE 的度数为_____°;

-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题
(1)元旦期间,“茂业“商场对某品牌羽绒服实行七折销售,张阿姨到该商场购买了一件该品牌的羽绒服发现比不打折时可省下240元,那么该品牌的标价是多少元?
(2)某公司共有工人40人,已知一个工人每小时可制造10个
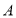 种零件或20个
种零件或20个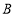 种零件,每个工人能而且只能制造其中的一种零件.
种零件,每个工人能而且只能制造其中的一种零件.①如果这些工人每小时能制造
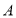 、
、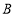 两种零件共550个,请问其中参加制造
两种零件共550个,请问其中参加制造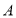 种零件的工人有多少人?
种零件的工人有多少人?②如果1个
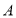 种零件与3个
种零件与3个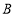 种零件组合后能形成一个整件,为使这些工人每小时制造出的零件都能恰好组合成整件,那么应安排多少工人制造
种零件组合后能形成一个整件,为使这些工人每小时制造出的零件都能恰好组合成整件,那么应安排多少工人制造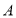 种零件?
种零件? -
科目: 来源: 题型:
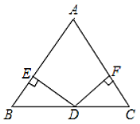
查看答案和解析>>【题目】如图,已知在
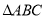 中,
中, ,
, 为
为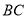 边的中点,过点
边的中点,过点 作
作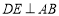 ,
,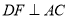 ,垂足分别为
,垂足分别为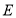 ,
, .
.
(1)求证:
 ;
;(2)若
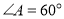 ,
, ,求
,求 的周长.
的周长.
相关试题

