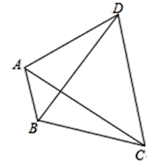
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AF交CD于点E,交BC的延长线于点F. 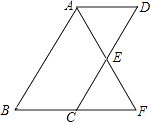
(1)求证:BF=CD;
(2)连接BE,若BE⊥AF,∠BFA=60°,BE=2 ![]() ,求平行四边形ABCD的周长.
,求平行四边形ABCD的周长. 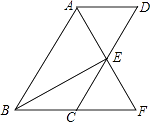
参考答案:
【答案】
(1)解:证明:∵四边形ABCD为平行四边形,
∴AB=CD,AD∥BC,
∴∠FAD=∠AFB,
又∵AF平分∠BAD,
∴∠FAD=∠FAB.
∴∠AFB=∠FAB.
∴AB=BF,
∴BF=CD
(2)解:∵由(1)知:AB=BF,
又∵∠BFA=60°,
∴△ABF为等边三角形,
∴AF=BF=AB,∠ABE=60°,
∵BE⊥AF,
∴点E是AF的中点.
∵在Rt△BEF中,∠BFA=60°,BE= ![]() ,
,
∴EF=2,BF=4,
∴AB=BF=4,
∵四边形BACD是平行四边形,
∴AB=CD,AD=BC,AB∥CD,
∴∠DCF=∠ABC=60°=∠F,
∴CE=EF,
∴△ECF是等边三角形,
∴CE=EF=CF=2,
∴BC=4﹣2=2,
∴平行四边形ABCD的周长为2+2+4+4=12
【解析】(1.)根据平行四边形的性质得出AB=CD,AD∥BC,求出∠FAD=∠AFB,根据角平分线定义得出∠FAD=∠FAB,求出∠AFB=∠FAB,即可得出答案; (2.)求出△ABF为等边三角形,根据等边三角形的性质得出AF=BF=AB,∠ABE=60°,在Rt△BEF中,∠BFA=60°,BE= ![]() ,解直角三角形求出EF=2,BF=4,AB=BF=4,BC=AD=2,即可得出答案.
,解直角三角形求出EF=2,BF=4,AB=BF=4,BC=AD=2,即可得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y=
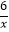 相交于点A(m,3),B(﹣6,n),与x轴交于点C.
相交于点A(m,3),B(﹣6,n),与x轴交于点C. 
(1)求直线y=kx+b(k≠0)的解析式;
(2)若点P在x轴上,且S△ACP= S△BOC , 求点P的坐标(直接写出结果).
S△BOC , 求点P的坐标(直接写出结果). -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程或方程组解应用题: 在某场CBA比赛中,某位运动员的技术统计如表所示:
技术
上场时间(分钟)
出手投篮(次)
投中
(次)罚球得分(分)
篮板
(个)助攻(次)
个人总得分(分)
数据
38
27
11
6
3
4
33
注:(i)表中出手投篮次数和投中次数均不包括罚球;
(ii)总得分=两分球得分+三分球得分+罚球得分.
根据以上信息,求本场比赛中该运动员投中两分球和三分球各几个. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,A(﹣2,0),B(0,4),以B点为直角顶点在第二象限作等腰直角△ABC.
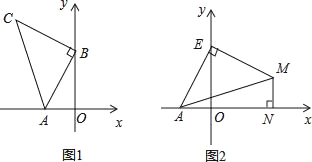
(1)求C点的坐标;
(2)在坐标平面内是否存在一点P,使△PAB与△ABC全等?若存在,求出P点坐标,若不存在,请说明理由;
(3)如图2,点E为y轴正半轴上一动点,以E为直角顶点作等腰直角△AEM,过M作MN⊥x轴于N,求OE﹣MN的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ABC=120°,BD平分∠ABC,∠DAC=60°,若AB=2,BC=3,则BD的长是( )
A. 5 B. 7 C. 8 D. 9
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料: “共享单车”是指企业与政府合作,在校园、地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车共享的一种服务,是共享经济的一种新形态.共享单车的出现让更多的用户有了更好的代步选择.自行车也代替了一部分公共交通甚至打车的出行.
Quest Mobile监测的M型与O型单车从2016年10月﹣﹣2017年1月的月度用户使用情况如表所示:
根据以上材料解答下列问题:
(1)仔细阅读上表,将O型单车总用户数用折线图表示出来,并在图中标明相应数据;
(2)根据图表所提提供的数据,选择你所感兴趣的方面,写出一条你发现的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】苏果超市用2730元购进A、B两种型号的保温杯共60个,这两种型号的保温杯的进价、标价如表所示:
价格类型
A型
B型
进价
 元
元 个
个
35
65
标价
 元
元 个
个
50
100
 求这两种型号的保温杯各购进多少个?
求这两种型号的保温杯各购进多少个? 若A型保温杯按标价的9折出售,要使这批保温杯全部售出后超市获得810元的利润,则B型保温杯应按标价的几折出售?
若A型保温杯按标价的9折出售,要使这批保温杯全部售出后超市获得810元的利润,则B型保温杯应按标价的几折出售?
相关试题

