【题目】下列命题:
①如果a,b,c为一组勾股数,那么4a,4b,4c仍是勾股数;
②如果直角三角形的两边是5、12,那么斜边必是13;
③如果一个三角形的三边是12、25、21,那么此三角形必是直角三角形;
④一个等腰直角三角形的三边是a,b,c(a>b=c),那么a2:b2:c2=2:1:1.
其中正确的是( )
A.①② B.①③ C.①④ D.②④
参考答案:
【答案】C
【解析】
试题分析:根据勾股定理对①进行判断;利用分类讨论的思想和勾股定理对②进行判断;根据勾股定理的逆定理对③进行判断;根据等腰直角三角形的性质对④进行判断.
解:如果a,b,c为一组勾股数,那么4a,4b,4c仍是勾股数,所以①正确;
如果直角三角形的两边是5、12,那么斜边是13或![]() ,所以②错误;
,所以②错误;
如果一个三角形的三边是12、25、21,那么此三角形不是直角三角形,所以③错误;
一个等腰直角三角形的三边是a,b,c(a>b=c),那么a2:b2:c2=2:1:1,所以④正确.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】神农尝百草,泡泡青菜便是其中之一,小随同学利用假期开网店批发出售泡泡青菜,他打出促销广告:最优质泡泡青菜35箱,每箱售价30元,若一次性购买不超过10箱时,售价不变;若一次性购买超过10箱时,没多买1箱,所买的每箱泡泡青菜的售价均降低0.3元.已知该青菜成本是每箱20元,若不计其他费用,设顾客一次性购买泡泡青菜x(x为整数)箱时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少箱时,该网店从中获利最多,最多是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
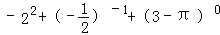
(2)(﹣a)2
 a4÷a3
a4÷a3(3)(2x﹣1)(x﹣3)
(4)(3x﹣2y)2(3x+2y)2
(5)(x﹣2y+4)(x﹣2y﹣4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠ABC=64°,∠AEB=70°.
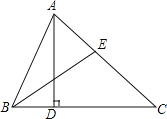
(1)求∠CAD的度数;
(2)若点F为线段BC上的任意一点,当△EFC为直角三角形时,求∠BEF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
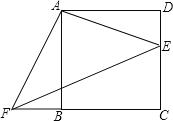
(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.

(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠A=145°,∠D=75°.
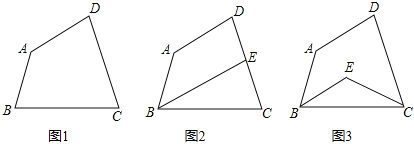
(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
相关试题

