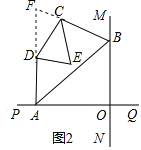
【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.
参考答案:
【答案】(1)∠AEB的大小不变135°;(2)∠CED的大小不变67.5°;(3)60°或45°.
【解析】
试题分析:(1)根据直线MN与直线PQ垂直相交于O可知∠AOB=90°,再由AE、BE分别是∠BAO和∠ABO角的平分线得出∠BAE=![]() ∠OAB,∠ABE=
∠OAB,∠ABE=![]() ∠ABO,由三角形内角和定理即可得出结论;
∠ABO,由三角形内角和定理即可得出结论;
(2)延长AD、BC交于点F,根据直线MN与直线PQ垂直相交于O可得出∠AOB=90°,进而得出∠OAB+∠OBA=90°,故∠PAB+∠MBA=270°,再由AD、BC分别是∠BAP和∠ABM的角平分线,可知∠BAD=![]() ∠BAP,∠ABC=
∠BAP,∠ABC=![]() ∠ABM,由三角形内角和定理可知∠F=45°,再根据DE、CE分别是∠ADC和∠BCD的角平分线可知∠CDE+∠DCE=112.5°,进而得出结论;
∠ABM,由三角形内角和定理可知∠F=45°,再根据DE、CE分别是∠ADC和∠BCD的角平分线可知∠CDE+∠DCE=112.5°,进而得出结论;
(3))由∠BAO与∠BOQ的角平分线相交于E可知∠EAO=![]() ∠BAO,∠EOQ=
∠BAO,∠EOQ=![]() ∠BOQ,进而得出∠E的度数,由AE、AF分别是∠BAO和∠OAG的角平分线可知∠EAF=90°,在△AEF中,由一个角是另一个角的3倍分四种情况进行分类讨论.
∠BOQ,进而得出∠E的度数,由AE、AF分别是∠BAO和∠OAG的角平分线可知∠EAF=90°,在△AEF中,由一个角是另一个角的3倍分四种情况进行分类讨论.
解:(1)∠AEB的大小不变,
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∵AE、BE分别是∠BAO和∠ABO角的平分线,
∴∠BAE=![]() ∠OAB,∠ABE=
∠OAB,∠ABE=![]() ∠ABO,
∠ABO,
∴∠BAE+∠ABE=![]() (∠OAB+∠ABO)=45°,
(∠OAB+∠ABO)=45°,
∴∠AEB=135°;
(2)∠CED的大小不变.
延长AD、BC交于点F.
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∴∠PAB+∠MBA=270°,
∵AD、BC分别是∠BAP和∠ABM的角平分线,
∴∠BAD=![]() ∠BAP,∠ABC=
∠BAP,∠ABC=![]() ∠ABM,
∠ABM,
∴∠BAD+∠ABC=![]() (∠PAB+∠ABM)=135°,
(∠PAB+∠ABM)=135°,
∴∠F=45°,
∴∠FDC+∠FCD=135°,
∴∠CDA+∠DCB=225°,
∵DE、CE分别是∠ADC和∠BCD的角平分线,
∴∠CDE+∠DCE=112.5°,
∴∠E=67.5°;
(3)∵∠BAO与∠BOQ的角平分线相交于E,
∴∠EAO=![]() ∠BAO,∠EOQ=
∠BAO,∠EOQ=![]() ∠BOQ,
∠BOQ,
∴∠E=∠EOQ﹣∠EAO=![]() (∠BOQ﹣∠BAO)=
(∠BOQ﹣∠BAO)=![]() ∠ABO,
∠ABO,
∵AE、AF分别是∠BAO和∠OAG的角平分线,
∴∠EAF=90°.
在△AEF中,
∵有一个角是另一个角的3倍,故有:
①∠EAF=3∠E,∠E=30°,∠ABO=60°;
②∠EAF=3∠F,∠E=60°,∠ABO=120°;
③∠F=3∠E,∠E=22.5°,∠ABO=45°;
④∠E=3∠F,∠E=67.5°,∠ABO=135°.
∴∠ABO为60°或45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠ABC=64°,∠AEB=70°.
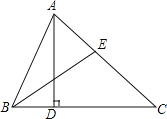
(1)求∠CAD的度数;
(2)若点F为线段BC上的任意一点,当△EFC为直角三角形时,求∠BEF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:
①如果a,b,c为一组勾股数,那么4a,4b,4c仍是勾股数;
②如果直角三角形的两边是5、12,那么斜边必是13;
③如果一个三角形的三边是12、25、21,那么此三角形必是直角三角形;
④一个等腰直角三角形的三边是a,b,c(a>b=c),那么a2:b2:c2=2:1:1.
其中正确的是( )
A.①② B.①③ C.①④ D.②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
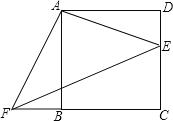
(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠A=145°,∠D=75°.
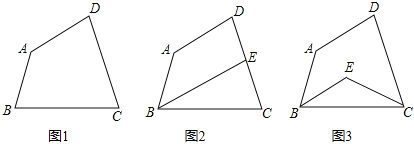
(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算a3a2正确的是( )
A. a B. a5 C. a6 D. a9
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线y=﹣
 x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.
x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.
(1)求抛物线的解析式;
(2)在AC上方的抛物线上有一动点P.
①如图1,当点P运动到某位置时,以AP,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点P的坐标;
②如图2,过点O,P的直线y=kx交AC于点E,若PE:OE=3:8,求k的值.
相关试题

