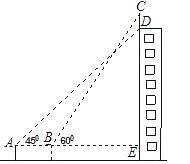
【题目】如图,某幢大楼顶部有一块广告牌CD,甲、乙两人分别在A、B两处,甲测得点D的仰角为45°,乙测得点C的仰角为60°,已知两人使用的测角仪的高度AF、BG相等,且A、B、E三点在一条直线上,AB=8m,BE=15m.求广告牌CD的高(精确到1m).
参考答案:
【答案】3m.
【解析】试题分析:在Rt△ADE和Rt△BCE中,分别求出CE和DE的长度,然后可求得CD=CE﹣DE.
试题解析:解:∵AB=8m,BE=15m,∴AE=AB+BE=23m.在Rt△ADE中,∵∠DAE=45°,∴DE=AE=23m.在Rt△CBE中,∵∠CBE=60°,BE=15m,∴CE=BEtan60°=15![]() m,则CD=CE﹣DE=15
m,则CD=CE﹣DE=15![]() ﹣23≈3(m).
﹣23≈3(m).
答:广告牌CD的高为3m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中央电视台的“朗读者”节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对七年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本书最少的有5本,最多的有8本,并根据调查结果绘制了不完整的图表,如下所示:
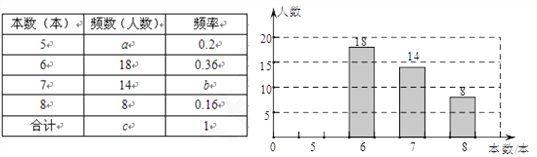
(1)统计表中的a=________,b=___________,c=____________;
(2)请将频数分布表直方图补充完整;
(3)求所有被调查学生课外阅读的平均本数;
(4)若该校七年级共有1200名学生,请你分析该校七年级学生课外阅读7本及以上的人数.
-
科目: 来源: 题型:
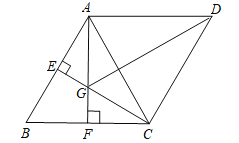
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别是AB、BC的中点,CE⊥AB,垂足为E,AF⊥BC,垂足为F,AF与CE相交于点G.
(1)证明:△CFG≌△AEG.
(2)若AB=4,求四边形AGCD的对角线GD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小聪在复习过程中,发现数轴上线段的长度可以用线段端点表示的数进行减法运算得到,例:
如图1,线段
 ,线段
,线段 ,
,
线段
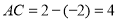 ,线段
,线段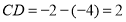
结论:数轴上任意两点表示的数分别为:
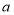 ,
,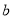 (
( ),则这两点间的距离为:
),则这两点间的距离为: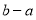 (即:较大的数减去较小的数).
(即:较大的数减去较小的数).尝试应用:
(1)若数轴上点
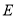 ,点
,点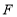 代表的数分别是-3,-1,则
代表的数分别是-3,-1,则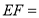 ______.
______.(2)把一条数轴在数
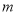 处对折,表示-9和3两数的点恰好互相重合,此时
处对折,表示-9和3两数的点恰好互相重合,此时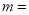 ______.
______.(3)数轴上的两个点之间的距离为6,其中一个点表示的数为3,另一个点表示的数为
 ,则
,则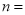 ______.
______.问题解决:
(4)如图2,点
 表示数
表示数 ,点
,点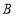 表示-2,点
表示-2,点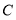 表示
表示 且
且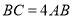 ,问点
,问点 和点
和点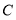 分别表示什么数?为什么?
分别表示什么数?为什么?
(5)上述(4)的条件下,图2所示的数轴上,是否存在满足条件的点
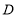 ,使用
,使用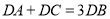 ?
?若存在,请直接写出
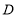 所表示的数,若不存在,请说明理由?(点
所表示的数,若不存在,请说明理由?(点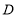 不与点
不与点 ,点
,点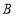 ,点
,点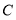 重合)
重合) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不一定正确的是 ( )
A..若 x y ,则 x c=y cB.若 x y ,则 xc yc
C.若 x y ,则
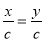 D.若
D.若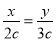 ,则 3x 2 y
,则 3x 2 y -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:a是单项式-xy2的系数,b是最小的正整数,c是多项式2m2n-m3n2-m-2的次数.请回答下列问题:
(1)请直接写出a、b、c的值.a= ,b= ,c= .
(2)数轴上,a、b、c三个数所对应的点分别为A、B、C,点A、B、C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动,假设t秒钟过后,若点B与点c之间的距离表示为BC,点A与点C之间的距离表示为AC,点A与点C之间的距离表示为AC.
①t秒钟过后,AC的长度为 (用含t的关系式表示);
②请问:BC-AB的值是否会随着时间t的变化而改变?若变化,请说明理由;若不变,请求出其值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知O是直线CD上的点,OA平分∠BOC,OE平分∠BOD,∠AOC=35°,

(1) 求∠BOE的度数,
(2)求∠COE的度数.
相关试题

