【题目】已知:a是单项式-xy2的系数,b是最小的正整数,c是多项式2m2n-m3n2-m-2的次数.请回答下列问题:
(1)请直接写出a、b、c的值.a= ,b= ,c= .
(2)数轴上,a、b、c三个数所对应的点分别为A、B、C,点A、B、C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动,假设t秒钟过后,若点B与点c之间的距离表示为BC,点A与点C之间的距离表示为AC,点A与点C之间的距离表示为AC.
①t秒钟过后,AC的长度为 (用含t的关系式表示);
②请问:BC-AB的值是否会随着时间t的变化而改变?若变化,请说明理由;若不变,请求出其值.
参考答案:
【答案】(1)-1,1,5;(2)①4t+6;②不会变化,![]()
【解析】
(1)根据多项式、单项式、正整数的定义进行判断即可;
(2)①根据数轴上两点间的距离的求法进行求解;②求出![]() 的式子,看是否含有变量进行判断.
的式子,看是否含有变量进行判断.
(1)∵单项式![]() 的系数是-1
的系数是-1
∴![]()
∵最小的正整数是![]()
∴![]()
∵多项式![]() 的次数是5次
的次数是5次
∴![]() ;
;
(2)①∵点A与点C之间初始的距离是![]() ,且它们的运动方向是背离的
,且它们的运动方向是背离的
∴![]() ;
;
②不会变化,理由如下:
由题得:![]() ,
,![]() ,
,
则![]()
∴BC-AB的值不会随着时间t的变化而改变.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小聪在复习过程中,发现数轴上线段的长度可以用线段端点表示的数进行减法运算得到,例:
如图1,线段
 ,线段
,线段 ,
,
线段
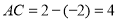 ,线段
,线段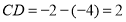
结论:数轴上任意两点表示的数分别为:
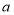 ,
,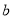 (
( ),则这两点间的距离为:
),则这两点间的距离为: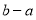 (即:较大的数减去较小的数).
(即:较大的数减去较小的数).尝试应用:
(1)若数轴上点
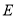 ,点
,点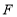 代表的数分别是-3,-1,则
代表的数分别是-3,-1,则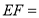 ______.
______.(2)把一条数轴在数
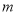 处对折,表示-9和3两数的点恰好互相重合,此时
处对折,表示-9和3两数的点恰好互相重合,此时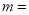 ______.
______.(3)数轴上的两个点之间的距离为6,其中一个点表示的数为3,另一个点表示的数为
 ,则
,则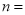 ______.
______.问题解决:
(4)如图2,点
 表示数
表示数 ,点
,点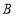 表示-2,点
表示-2,点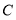 表示
表示 且
且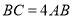 ,问点
,问点 和点
和点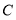 分别表示什么数?为什么?
分别表示什么数?为什么?
(5)上述(4)的条件下,图2所示的数轴上,是否存在满足条件的点
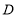 ,使用
,使用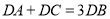 ?
?若存在,请直接写出
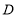 所表示的数,若不存在,请说明理由?(点
所表示的数,若不存在,请说明理由?(点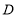 不与点
不与点 ,点
,点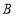 ,点
,点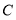 重合)
重合) -
科目: 来源: 题型:
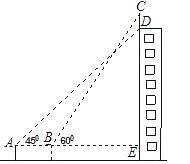
查看答案和解析>>【题目】如图,某幢大楼顶部有一块广告牌CD,甲、乙两人分别在A、B两处,甲测得点D的仰角为45°,乙测得点C的仰角为60°,已知两人使用的测角仪的高度AF、BG相等,且A、B、E三点在一条直线上,AB=8m,BE=15m.求广告牌CD的高(精确到1m).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不一定正确的是 ( )
A..若 x y ,则 x c=y cB.若 x y ,则 xc yc
C.若 x y ,则
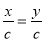 D.若
D.若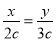 ,则 3x 2 y
,则 3x 2 y -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知O是直线CD上的点,OA平分∠BOC,OE平分∠BOD,∠AOC=35°,

(1) 求∠BOE的度数,
(2)求∠COE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=
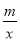 (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.
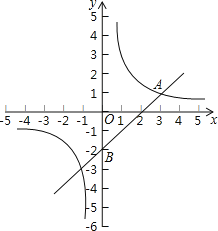
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习有理数的乘法后,老师给同学们这样一道题目:计算:49
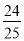 ×(﹣5),看谁算的又快又对,有两位同学的解法如下:
×(﹣5),看谁算的又快又对,有两位同学的解法如下: 小明:原式=﹣
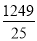 ×5=﹣
×5=﹣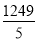 =﹣249
=﹣249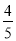 ;
; 小军:原式=(49+
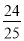 )×(﹣5)=49×(﹣5)+
)×(﹣5)=49×(﹣5)+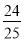 ×(﹣5)=﹣249
×(﹣5)=﹣249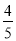 ;
; (1)对于以上两种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,你认为还有更好的方法吗?如果有,请把它写出来;
(3)用你认为最合适的方法计算:19
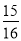 ×(﹣8)
×(﹣8)
相关试题

