【题目】如图,已知O是直线CD上的点,OA平分∠BOC,OE平分∠BOD,∠AOC=35°,

(1) 求∠BOE的度数,
(2)求∠COE的度数.
参考答案:
【答案】(1)∠BOE=55°;(2)∠COE=125°.
【解析】
(1)根据角平分线的定义求出∠BOC的度数,根据平角的定义求出∠BOD的度数,再根据角平分线的定义计算即可;
(2)根据∠COE=∠BOC+∠BOE列式计算即可.
解:(1)∵OA平分∠BOC,∠AOC=35°,
∴∠BOC=2∠AOC=70°,
∴∠BOD=180°-70°=110°,
∵OE平分∠BOD,
∴∠BOE=![]() ∠BOD=55°;
∠BOD=55°;
(2)∵∠BOC=70°,∠BOE=55°,
∴∠COE=∠BOC+∠BOE=125°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某幢大楼顶部有一块广告牌CD,甲、乙两人分别在A、B两处,甲测得点D的仰角为45°,乙测得点C的仰角为60°,已知两人使用的测角仪的高度AF、BG相等,且A、B、E三点在一条直线上,AB=8m,BE=15m.求广告牌CD的高(精确到1m).
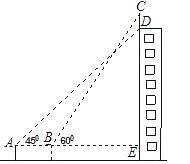
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不一定正确的是 ( )
A..若 x y ,则 x c=y cB.若 x y ,则 xc yc
C.若 x y ,则
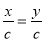 D.若
D.若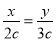 ,则 3x 2 y
,则 3x 2 y -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:a是单项式-xy2的系数,b是最小的正整数,c是多项式2m2n-m3n2-m-2的次数.请回答下列问题:
(1)请直接写出a、b、c的值.a= ,b= ,c= .
(2)数轴上,a、b、c三个数所对应的点分别为A、B、C,点A、B、C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动,假设t秒钟过后,若点B与点c之间的距离表示为BC,点A与点C之间的距离表示为AC,点A与点C之间的距离表示为AC.
①t秒钟过后,AC的长度为 (用含t的关系式表示);
②请问:BC-AB的值是否会随着时间t的变化而改变?若变化,请说明理由;若不变,请求出其值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=
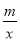 (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.
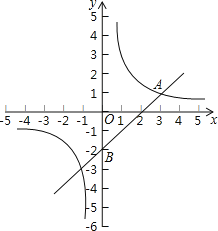
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习有理数的乘法后,老师给同学们这样一道题目:计算:49
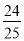 ×(﹣5),看谁算的又快又对,有两位同学的解法如下:
×(﹣5),看谁算的又快又对,有两位同学的解法如下: 小明:原式=﹣
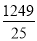 ×5=﹣
×5=﹣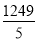 =﹣249
=﹣249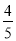 ;
; 小军:原式=(49+
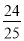 )×(﹣5)=49×(﹣5)+
)×(﹣5)=49×(﹣5)+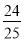 ×(﹣5)=﹣249
×(﹣5)=﹣249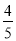 ;
; (1)对于以上两种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,你认为还有更好的方法吗?如果有,请把它写出来;
(3)用你认为最合适的方法计算:19
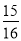 ×(﹣8)
×(﹣8) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,对角线AC、BD相交于点O,点P是线段AD上一动点(不与与点D重合),PO的延长线交BC于Q点.
(1)求证:四边形PBQD为平行四边形.
(2)若AB=6cm,AD=8cm,P从点A出发.以1cm/秒的速度向点D匀速运动.设点P运动时间为t秒,问四边形PBQD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.

相关试题

