【题目】如图1,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.

(1)求证:△DEC≌△EDA;
(2)求DF的值;
(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其顶点Q落在线段AE上,定点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的面积最大?并求出其最大值.
参考答案:
【答案】(1)证明见解析;(2)![]() .(3)PE=
.(3)PE=![]() 时,矩形PQMN的面积最大,最大面积为3.
时,矩形PQMN的面积最大,最大面积为3.
【解析】
试题分析:(1)由矩形和翻折的性质可知AD=CE,DC=EA,根据“SSS”可求得△DEC≌△EDA;
(2)根据勾股定理即可求得.
(3)由矩形PQMN的性质得PQ∥CA,所以![]() ,从而求得PQ,由PN∥EG,得出
,从而求得PQ,由PN∥EG,得出![]() ,求得PN,然后根据矩形的面积公式求得解析式,即可求得.
,求得PN,然后根据矩形的面积公式求得解析式,即可求得.
试题解析:(1)由矩形和翻折的性质可知:AD=CE,DC=EA,
在△ADE与△CED中,

∴△DEC≌△EDA(SSS);
(2)如图1,
∵∠ACD=∠BAC,∠BAC=∠CAE,
∴∠ACD=∠CAE,
∴AF=CF,
设DF=x,则AF=CF=4-x,
在Rt△ADF中,AD2+DF2=AF2,
即32+x2=(4-x)2,
解得:x=![]() ,
,
即DF=![]() .
.
(3)如图2,

由矩形PQMN的性质得PQ∥CA
∴![]()
又∵CE=3,AC=![]() =5
=5
设PE=x(0<x<3),则![]() ,即PQ=
,即PQ=![]() x
x
过E作EG⊥AC于G,则PN∥EG,
∴![]()
又∵在Rt△AEC中,EGAC=AECE,解得EG=![]() ,
,
∴![]() =
=![]() ,即PN=
,即PN=![]() (3-x),
(3-x),
设矩形PQMN的面积为S,
则S=PQPN=-![]() x2+4x=-
x2+4x=-![]() (x-
(x-![]() )2+3(0<x<3)
)2+3(0<x<3)
所以当x=![]() ,即PE=
,即PE=
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业今年1月份产值为x万元,2月份比1月份减少了10%,3月份比2月份增加了15%,则3月份的产值是( )
A. (1-10%)(1+15%)x万元 B. (1-10%+15%)x万元
C. (x-10%)(x+15%)万元 D. (1+10%-15%)x万元
-
科目: 来源: 题型:
查看答案和解析>>【题目】由四舍五入法得到的近似数8.8×103,下列说法中正确的是 ( )
A. 精确到十分位 B. 精确到个位 C. 精确到百位 D. 精确到千位
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=
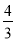 x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.
x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.
(1)求该二次函数的解析式及点C的坐标;
(2)当点P运动到B点时,点Q停止运动,这时,在x轴上是否存在点E,使得以A,E,Q为顶点的三角形为等腰三角形?若存在,请求出E点坐标;若不存在,请说明理由.
(3)当P,Q运动到t秒时,△APQ沿PQ翻折,点A恰好落在抛物线上D点处,请判定此时四边形APDQ的形状,并求出D点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件是必然事件的是( )
A. 某运动员射击一次击中靶心
B. 抛一枚硬币,正面朝上
C. 3个人分成两组,一定有2个人分在一组
D. 明天一定是晴天
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:x3﹣xy2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校进行了一次数学成绩测试,甲、乙两班学生的成绩如下表所示(满分120分):
班级
平均分
众数
方差
甲
101
90
2.65
乙
102
87
2.38
你认为哪一个班的成绩更好一些?并说明理由.
答:_____班(填“甲”或“乙”),理由是_______________________________.
相关试题

