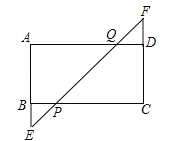
【题目】如图,矩形ABCD中,延长AB至E,延长CD至F,BE=DF,连接EF,与BC、AD分别相交于P、Q两点.
(1)求证:CP=AQ;
(2)若BP=1,PQ=![]() ,∠AEF=45°,求矩形ABCD的面积.
,∠AEF=45°,求矩形ABCD的面积.
参考答案:
【答案】(1)证明见解析;(2)8.
【解析】
试题分析:(1)由矩形的性质得出∠A=∠ABC=∠C=∠ADC=90°,AB=CD,AD=BC,AB∥CD,AD∥BC,证出∠E=∠F,AE=CF,由ASA证明△CFP≌△AEQ,即可得出结论;
(2)证明△BEP、△AEQ是等腰直角三角形,得出BE=BP=1,AQ=AE,求出PE=![]() BP=
BP=![]() ,得出EQ=PE+PQ=
,得出EQ=PE+PQ=![]() ,由等腰直角三角形的性质和勾股定理得出AQ=AE=3,求出AB=AE﹣BE=2,DQ=BP=1,得出AD=AQ+DQ=4,即可求出矩形ABCD的面积.
,由等腰直角三角形的性质和勾股定理得出AQ=AE=3,求出AB=AE﹣BE=2,DQ=BP=1,得出AD=AQ+DQ=4,即可求出矩形ABCD的面积.
试题解析:(1)证明:∵四边形ABCD是矩形,∴∠A=∠ABC=∠C=∠ADC=90°,AB=CD,AD=BC,AB∥CD,AD∥BC,∴∠E=∠F,∵BE=DF,∴AE=CF,在△CFP和△AEQ中,∵∠C=∠A,CF=AE,∠F=∠E,∴△CFP≌△AEQ(ASA),∴CP=AQ;
(2)解:∵AD∥BC,∴∠PBE=∠A=90°,∵∠AEF=45°,∴△BEP、△AEQ是等腰直角三角形,∴BE=BP=1,AQ=AE,∴PE=![]() BP=
BP=![]() ,∴EQ=PE+PQ=
,∴EQ=PE+PQ=![]() =
=![]() ,∴AQ=AE=3,∴AB=AE﹣BE=2,∵CP=AQ,AD=BC,∴DQ=BP=1,∴AD=AQ+DQ=3+1=4,∴矩形ABCD的面积=ABAD=2×4=8.
,∴AQ=AE=3,∴AB=AE﹣BE=2,∵CP=AQ,AD=BC,∴DQ=BP=1,∴AD=AQ+DQ=3+1=4,∴矩形ABCD的面积=ABAD=2×4=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解一元二次方程x2+2x-5=0,此方程可变形为( )
A.(x-1)2=6B.(x+1)2=6C.(x+1)2=4D.(x-1)2=1
-
科目: 来源: 题型:
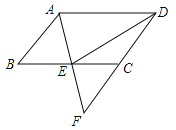
查看答案和解析>>【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店需要购进甲、乙两种商品共180件,其进价和售价如表:(注:获利=售价﹣进价)
甲
乙
进价(元/件)
14
35
售价(元/件)
20
43
(1)若商店计划销售完这批商品后能获利1240元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于5040元,且销售完这批商品后获利多于1312元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案. -
科目: 来源: 题型:
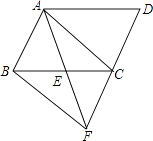
查看答案和解析>>【题目】如图,在ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC.求证:∠BAC=∠BFC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“两直线平行,内错角相等”的题设是_________,结论是_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E,F分别是AB,CD的中点,G,H分别是AF,CE的中点,连结EG,FH.

(1)四边形EHFG是不是平行四边形?如果是,请给出证明;如果不是,请说明理由;
(2)求四边形EHFG的面积与平行四边形ABCD的面积之比.
相关试题

