【题目】(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,EF分别是 BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是延长FD到点G,使DG=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
探索延伸:
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由.
∠BAD,上述结论是否仍然成立,并说明理由.

参考答案:
【答案】问题背景:BE +DF =EF;探索延伸:结论仍然成立,理由见解析.
【解析】
问题背景:证明△ABE≌△ADG,可得AE=AG,再证明△AEF≌△AGF,可得EF=FG,即可解题;
探索延伸:延长FD到G,使DG=BE,连接AG,根据同角的补角相等求出∠B=∠ADG,然后利用“边角边”证明△ABE和△ADG全等,根据全等三角形对应边相等可得AE=AG,∠BAE=∠DAG,再求出∠EAF=∠GAF,然后利用“边角边”证明△AEF和△GAF全等,根据全等三角形对应边相等可得EF=GF,然后求解即可;
问题背景:在△ABE和△ADG中,
 ,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
 ,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
故答案为:EF=BE+DF;
探索延伸: 结论仍然成立,理由如下:
如图②,延长FD到G,使DG =BE,连接AG,

∵∠B +∠ADC =180°,∠ADC +∠ADG =180°,
∴∠B =∠ADG,
在△ABE和△ADG中,
 ,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
 ,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小颖为妈妈准备了一份生日礼物,礼物外包装盒为长方体形状,长、宽、高分别为
 、
、 、
、
 ,为了美观,小颖决定在包装盒外用丝带打包装饰,她发现,可以用如图所示的三种打包方式,所需丝带的长度分别为
,为了美观,小颖决定在包装盒外用丝带打包装饰,她发现,可以用如图所示的三种打包方式,所需丝带的长度分别为 ,
, ,
, (不计打结处丝带长度)
(不计打结处丝带长度)
(1)用含
 、
、 、
、 的代数式分别表示
的代数式分别表示 ,
, ,
, ;
;(2)方法简介:
要比较两数
 与
与 大小,我们可以将
大小,我们可以将 与
与 作差,结果可能出现三种情况:
作差,结果可能出现三种情况:①
 ,则
,则 ;
;②
 ,则
,则 ;
;③
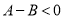 ,则
,则 ;
;我们将这种比较大小的方法叫做“作差法”.
请帮小颖选出最节省丝带的打包方式,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,两线相交于F点.
(1)若∠BAC=60°,∠C=70°,求∠AFB的大小;
(2)若D是BC的中点,∠ABE=30°,求证:△ABC是等边三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市组织学术研讨会,需租用客车接送参会人员往返宾馆和观摩地点,客车租赁公司现有
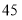 座和
座和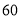 座两种型号的客车可供租用.
座两种型号的客车可供租用.(1)已知
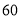 座的客车每辆每天的租金比
座的客车每辆每天的租金比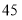 座的贵
座的贵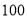 元,会务组第一天在这家公司租了
元,会务组第一天在这家公司租了 辆
辆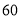 座和
座和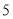 辆
辆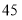 座的客车.一天的租金为
座的客车.一天的租金为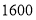 元,求
元,求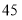 座和
座和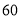 座的客车每辆每天的租金各是多少元?
座的客车每辆每天的租金各是多少元?(2)由于第二天参会人员发生了变化,因此会务纽需重新确定租车方案.
方案1:若只租用
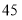 座的客车,会有一辆客车空出
座的客车,会有一辆客车空出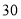 个座位;
个座位;方案2:若只租用
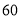 座客车,正好坐满且比只租用
座客车,正好坐满且比只租用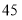 座的客车少用两辆.
座的客车少用两辆.①请计算方案1、2的费用;
②从经济角度考虑,还有方案3吗?如果你是会务纽负责人,应如何确定最终租车方案,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点
 为线段
为线段 上一点,一副直角三角板的直角顶点与点
上一点,一副直角三角板的直角顶点与点 重合,直角边
重合,直角边 、
、 在线段
在线段 上,
上, .
.
(1)将图1中的三角板
 绕着点
绕着点 沿顺时针方向旋转到如图2所示的位置,若
沿顺时针方向旋转到如图2所示的位置,若 ,则
,则 ________;猜想
________;猜想 与
与 的数量关系为________;
的数量关系为________;(2)将图1中的三角板
 绕着点
绕着点 沿逆时针方向按每秒
沿逆时针方向按每秒 的速度旋转一周,三角板
的速度旋转一周,三角板 不动,请问几秒时
不动,请问几秒时 所在的直线平分
所在的直线平分 ?
?(3)将图1中的三角板
 绕着点
绕着点 沿逆时针方向按每秒
沿逆时针方向按每秒 的速度旋转一周,同时三角板
的速度旋转一周,同时三角板 绕着点
绕着点 沿顺时针方向按每秒
沿顺时针方向按每秒 的速度旋转(随三角板
的速度旋转(随三角板 停止而停止),请计算几秒时
停止而停止),请计算几秒时 与
与 的角分线共线.
的角分线共线. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN( )

A.AM=CNB.AB=CD C.AM∥CN D.∠M=∠N
相关试题

