【题目】如图,某开发区计划在一块四边形的空地ABCD上种植草坪,已知∠A=90°,AB=4m,BC=12m,CD=13m,DA=3m,种植每平方米草皮的预算费用为300元,若第一年对草坪的保养费用占种植草皮总预算的4%,以后每年的保养费用都将在前一年的基础上递增2%,求第三年的草坪保养费用.

参考答案:
【答案】第三年的草坪保养费用是864元.
【解析】
通过分析可知,需要求得四边形的面积才能求得结果.连接BD,在直角三角形ABD中可求得BD的长,由BD、CD、BC的长度关系可得三角形DBC为一直角三角形,DC为斜边;由此看,四边形ABCD由Rt△ABD和Rt△DBC构成,则容易求解,再进一步得到第三年的草坪保养费用.
解:连接BD,
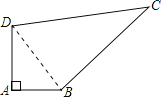
在Rt△ABD中,BD2=AB2+AD2=42+32=52,
在△CBD中,CD2=132,BC2=122,
而122+52=132,
即BD2+BC2=CD2,
∴∠DBC=90°,
S四边形ABCD=S△BAD+S△DBC=![]() ×4×3+
×4×3+![]() ×12×5=36.
×12×5=36.
所以需费用36×300×(4%+2%+2%)=864(元).
答:第三年的草坪保养费用是864元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知平行四边形ABCD顶点A的坐标为(2,6),点B在y轴上,且AD∥BC∥x轴,过B,C,D三点的抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,2),点F(m,6)是线段AD上一动点,直线OF交BC于点E.

(1)求抛物线的表达式;
(2)设四边形ABEF的面积为S,请求出S与m的函数关系式,并写出自变量m的取值范围;
(3)如图2,过点F作FM⊥x轴,垂足为M,交直线AC于P,过点P作PN⊥y轴,垂足为N,连接MN,直线AC分别交x轴,y轴于点H,G,试求线段MN的最小值,并直接写出此时m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,D、E是△ABC中BC边上的两点,AD=AE,要证明△ABE≌△ACD,应该再增加一个什么条件?请你增加这个条件后再给予证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用四块完全相同的小长方形拼成的一个“回形”正方形.

(1)用不同代数式表示图中的阴影部分的面积,你能得到怎样的等式:________;
(2)利用(1)中的结论.计算:
 ,
, ,求
,求 的值;
的值;(3)根据(1)的结论.若
 .求
.求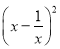 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、拆项法、字相乘法等等,将一个多项式适当分组后,可提公因式或运用公式继续分解的方法叫做分组分解.
例如:

利用这种分组的思想方法解决下列问题:
(1)分解因式
 ;
;(2)
 三边a,b,c满足
三边a,b,c满足 判断
判断 的形状,并说明理由.
的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了测量一个圆铁环的半径,某同学用了如下方法,将铁环平放在水平桌面上,用有一个角为30°的直角三角板和刻度尺按如图所示的方法得到相关数据,进而求出铁环半径,若测得PA=5cm,则铁环的半径是_____cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,点
,点 在
在 内,
内, ,
, ,点
,点 在
在 外,
外, ,
,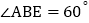 .
.(1)求
 的度数;
的度数;(2)判断
 的形状并加以证明;
的形状并加以证明;(3)连接
 ,若
,若 ,
, ,求
,求 的长.
的长.
相关试题

