【题目】△ABC中,∠ACB=90°,CB=6,AC=8,点D是AC上的一点,点E是BD上一点.
(1)如图(1),若点D在AB的垂直平分线上,求CD的长.
(2)如图(2),连接AE,若AE平分∠BAC,BE平分∠ABC,求点E到AC的距离.
(3)若点E到三角形两边的距离为1.5,求CD的长.(直接写出答案)

参考答案:
【答案】(1)![]() (2)2(3)3或2或
(2)2(3)3或2或![]()
【解析】
(1)由垂直平分线的性质可得BD=AD,AE=BE=5,设CD长为x,在![]() 中,由勾股定理列出方程即可解出CD的长;
中,由勾股定理列出方程即可解出CD的长;
(2)过点E作EF⊥AC于点F,EM⊥AB于点M,EN⊥BC于点N,由角平分线的性质可得EF=EM=EN,AE、BE、CE将![]() 分割成三个三角形,利用面积关系
分割成三个三角形,利用面积关系![]() =
= ![]() 可求出EF的长即为所求;
可求出EF的长即为所求;
(3)根据题意可分三种情况讨论:①当点E到AB和BC的距离为1.5时,过点D作DF⊥AB于点F,设CD为x,在![]() 中利用勾股定理可列出方程,求出x;②当点E到CB和CA的距离为1.5时,过点E作EM⊥AC于点M,EN⊥BC于点N,易知四边形CMEN为正方形,可得CM=1.5,由EM∥BC,可得
中利用勾股定理可列出方程,求出x;②当点E到CB和CA的距离为1.5时,过点E作EM⊥AC于点M,EN⊥BC于点N,易知四边形CMEN为正方形,可得CM=1.5,由EM∥BC,可得![]() ,进而得到
,进而得到![]() ,代入数据即可求出CD;③当点E到AB和AC的距离为1.5时,过点E作EM⊥AB于点M,EN⊥AC于点N,EF⊥BC于点F,易知四边形CNEF为矩形,根据面积关系
,代入数据即可求出CD;③当点E到AB和AC的距离为1.5时,过点E作EM⊥AB于点M,EN⊥AC于点N,EF⊥BC于点F,易知四边形CNEF为矩形,根据面积关系![]() =
= ![]() 可求EF的长度即为CN的长度,由EN∥BC,可得
可求EF的长度即为CN的长度,由EN∥BC,可得![]() 进而可得
进而可得![]() ,代入数据即可求出CD的长度.
,代入数据即可求出CD的长度.
(1)如图所示,设AB的垂直平分线为DE,垂足为E,
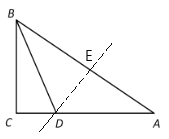
∵∠ACB=90°,CB=6,AC=8,
∴AB=![]() =10,
=10,
∵DE垂直平分AB,
∴BD=AD,AE=BE=![]() AB=5,
AB=5,
设CD=x,则AD=BD=8-x,在![]() 中,由勾股定理可得:
中,由勾股定理可得:
![]() ,
,
解得:![]() ,
,
∴点D在AB的垂直平分线上时,CD= ![]() ;
;
(2)如图所示,过点E作EF⊥AC于点F,EM⊥AB于点M,EN⊥BC于点N,连接CE,

∵AE平分∠BAC,EF⊥AC,EM⊥AB,
∴EF=EM,
∵BE平分∠ABC,EM⊥AB,EN⊥BC,
∴EM=EN,
∴EF=EM=EN,
设EF=EM=EN=x,则:
![]() =
= ![]()
即:![]() ×AC×BC=
×AC×BC= ![]() ×AC×EF+
×AC×EF+ ![]() ×AB×EM+
×AB×EM+ ![]() ×BC×EN,
×BC×EN,
6×8=8x+10x+6x,
解得:x=2,
∴点E到AC的距离为2;
(3)根据题意可分三种情况:
①如图所示,当点E到AB和BC的距离为1.5时,此时点E在∠CBA的角平分线上,即BD平分∠CBA,过点D作DF⊥AB于点F,

∵BD平分∠CBA,DF⊥AB,DC⊥BC,
∴CD=DF,
又∵∠C=∠DFB=90°,BD=BD,
∴![]() (HL),
(HL),
∴BF=BC=6,
∴AF=4,
设CD=x,则DF=x,AD=8-x,在![]() 中,由勾股定理可得:
中,由勾股定理可得:
![]() ,
,
解得:x=3,
∴当点E到AB和BC的距离为1.5时,CD=3;
②如图所示,当点E到CB和CA的距离为1.5时,此时点E在∠BCA的角平分线上,即CE平分∠BCA,过点E作EM⊥AC于点M,EN⊥BC于点N,此时EM=EN=1.5,EM∥BC,

∵∠NCM=90°, EM⊥AC,EN⊥BC,
∴四边形CMEN为矩形,
∵EM=EN
∴矩形CMEN为正方形,
∴CM=1.5,
设CD=x,则DM=x-1.5,
∵EM∥BC,
∴![]()
∴![]() ,
,
即: ![]() ,
,
解得:x=2,
∴当点E到CB和CA的距离为1.5时,CD=2;
③如图所示,当点E到AB和AC的距离为1.5时,此时点E在∠BAC的角平分线上,即AE平分∠BAC,过点E作EM⊥AB于点M,EN⊥AC于点N,EF⊥BC于点F,此时EM=EN=1.5,四边形CNEF为矩形,

∵![]() =
= ![]() ,
,
∴![]() ×AC×BC=
×AC×BC= ![]() ×AC×EN+
×AC×EN+ ![]() ×AB×EM+
×AB×EM+ ![]() ×BC×EF,
×BC×EF,
即6×8=8×1.5+10×1.5+6×EF,
解得:EF=![]() ,
,
∵四边形CNEF为矩形,
∴CN= EF=![]() ,
,
设CD=x,则DN=x-![]() ,
,
∵EN∥BC,
∴![]()
∴![]() ,
,
即: 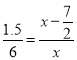 ,
,
解得:x=![]() ,
,
∴当点E到AB和AC的距离为1.5时,CD= ![]() .
.
综上所述,若点E到三角形两边的距离为1.5,CD的长为3或2或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校初三体育考试选择项目中,选择篮球项目和排球项目的学生比较多.为了解学生掌握篮球技巧和排球技巧的水平情况,进行了抽样调查,过程如下,请补充完整.
收集数据 从选择篮球和排球的学生中各随机抽取16人,进行了体育测试,测试成绩(十分制)如下:
排球 10 9.5 9.5 10 8 9 9.5 9
7 10 4 5.5 10 9.5 9.5 10
篮球 9.5 9 8.5 8.5 10 9.5 10 8
6 9.5 10 9.5 9 8.5 9.5 6
整理、描述数据 按如下分数段整理、描述这两组样本数据:
4.0≤x<5.5
5.5≤x<7.0
7.0≤x<8.5
8.5≤x<10
10
排球
1
1
2
7
5
篮球
(说明:成绩8.5分及以上为优秀,6分及以上为合格,6分以下为不合格.)
分析数据 两组样本数据的平均数、中位数、众数如下表所示:
项目
平均数
中位数
众数
排球
8.75
9.5
10
篮球
8.81
9.25
9.5
得出结论
(1)如果全校有160人选择
篮球项目,达到优秀的人数约为_____人; (2)初二年级的小明和小军看到上面数据后,小明说:排球项目整体水平较高.小军说:篮球项目整体水平较高.
你同意______ 的看法,理由为__________.(至少从两个不同的角度说明推断的合理性)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABO的边BO在x轴上,点A坐标(5,12),B(17,0),点C为BO边上一点,且AC=AO,点P为AB边上一点,且OP⊥AC.
(1)求出∠B的度数.
(2)试说明OA=OP.
(3)求点P的坐标及△PBO的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一玩具工厂用于生产的全部劳力为450个工时,原料为400个单位.生产一个小熊要使用15个工时、20个单位的原料,售价为80元;生产一个小猫要使用10个工时、5个单位的原料,售价为45元.在劳力和原料的限制下合理安排生产小熊、小猫的个数,可以使小熊和小猫的总售价尽可能高.请用你所学过的数学知识分析,总售价是否可能达到2200元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,甲、乙两个容器内都装了一定数量的水,现将甲容器中的水匀速注入乙容器中.图2中的线段AB,CD分别表示容器中的水的深度h(厘米)与注入时间t(分钟)之间的函数图象.下列结论错误的是( )
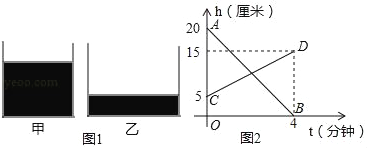
A. 注水前乙容器内水的高度是5厘米
B. 甲容器内的水4分钟全部注入乙容器
C. 注水2分钟时,甲、乙两个容器中的水的深度相等
D. 注水1分钟时,甲容器的水比乙容器的水深5厘米
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,如图所示,它是由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1,S2,S3,若正方形EFGH的边长为4,则S1+S2+S3的值为___________

-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=
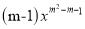 是反比例函数.
是反比例函数.(1)求m的值;
(2)指出该函数图象所在的象限,在每个象限内,y随x的增大如何变化?
(3)判断点(
 ,2)是否在这个函数的图象上.
,2)是否在这个函数的图象上.
相关试题

