【题目】在Rt△ABC中,∠A=90°,AB=AC=![]() +2,D是边AC上的动点,BD的垂直平分线交BC于点E,连接DE,若△CDE为直角三角形,则BE的长为_____.
+2,D是边AC上的动点,BD的垂直平分线交BC于点E,连接DE,若△CDE为直角三角形,则BE的长为_____.
参考答案:
【答案】![]() +1或2
+1或2
【解析】分析: 分两种情况:先根据勾股定理求斜边BC的长;
①当∠EDC=90°时,如图1,设BE=x,则DE=x,根据BC=BE+CE,列方程可得x的值;
②当∠DEC=90°时,如图2,同理可得BE的长,并知此时D与A重合.
详解: 分两种情况:
∵∠A=90°,AB=AC=![]() +2,
+2,
∴BC=![]() AB=2+2
AB=2+2![]() ,
,
①当∠EDC=90°时,如图1,
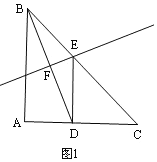
设BE=x,则DE=x,
∵∠C=45°,
∴△EDC是等腰直角三角形,
∴EC=![]() x,
x,
∴BC=BE+CE,
即2+2![]() =x+
=x+![]() x,x=2,
x,x=2,
∴BE=2,
②当∠DEC=90°时,如图2,
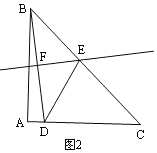
设BE=x,则DE=x,
∵∠C=45°,
∴△EDC是等腰直角三角形,
∴EC=x,
2x=2+2![]() ,x=
,x=![]() +1,
+1,
∴BE=![]() +1,(此种情况D与A重合)
+1,(此种情况D与A重合)
综上所述,BE的长为![]() +1或2.
+1或2.
故答案为:![]() +1或2.
+1或2.
点睛: 本题考查了线段垂直平分线的性质、等腰直角三角形的性质和判定、勾股定理,注意分类讨论△CDE为直角三角形时的直角顶点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
 的图象与二次函数
的图象与二次函数 (
(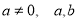 为常数)的图象交于
为常数)的图象交于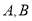 两点,且点
两点,且点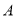 的坐标为
的坐标为 .
.(1)求出
 的值及点
的值及点 的坐标;
的坐标;(2)设
 ,若
,若 时,
时, 随着
随着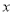 的增大而增大,且
的增大而增大,且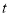 也随着
也随着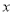 的增大而增大,求
的增大而增大,求 的最小值和
的最小值和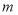 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某体育用品商店试销一款成本为 50 元的排球,规定试销期间单价不低于成本价,且获利不得高于 40%。经试销发现,销售量
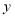 (个)与销售单价
(个)与销售单价 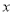 (元)之间满足如图所示的一次函数关系.
(元)之间满足如图所示的一次函数关系.(1)试确定
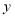 与
与 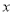 之间的函数关系式;
之间的函数关系式;(2)若该体育用品商店试销的这款排球所获得的利润为
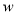 元,试写出利润
元,试写出利润 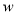 (元)与销售单价
(元)与销售单价 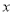 (元)之间的函数关系式;当试销单价定为多少元时,该商店可获最大利润?最大利润是多少元?
(元)之间的函数关系式;当试销单价定为多少元时,该商店可获最大利润?最大利润是多少元?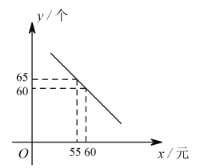
-
科目: 来源: 题型:
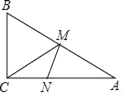
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=4,M是AB边上一动点,N是AC边上的一动点,则MN+MC的最小值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们约定:对角线相等的四边形称之为:“等线四边形”。
(1)①在“平行四边形、菱形、矩形、正方形”中一定是“等线四边形”的是___________________;
②如图1,若四边形
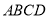 是“等线四边形”,
是“等线四边形”, 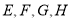 分别是边
分别是边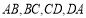 的中点,依次连接
的中点,依次连接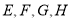 ,得到四边形
,得到四边形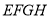 ,请判断四边形
,请判断四边形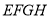 的形状:______________________;
的形状:______________________;(2)如图2,在平面直角坐标系
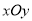 中,已知
中,已知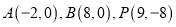 ,以
,以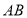 为直径作圆,该圆与
为直径作圆,该圆与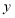 轴的正半轴交于点
轴的正半轴交于点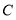 ,若
,若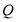 为坐标系中一动点,且四边形
为坐标系中一动点,且四边形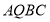 为“等线四边形”。当
为“等线四边形”。当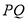 的长度最短时,求经过
的长度最短时,求经过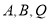 三点的抛物线的解析式;
三点的抛物线的解析式;(3)如图3,在平面直角坐标系
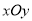 中,四边形
中,四边形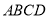 是“等线四边形”,
是“等线四边形”, 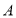 在
在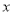 轴的负半轴上,
轴的负半轴上,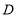 在
在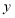 轴的负半轴上,且
轴的负半轴上,且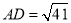 。点
。点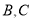 分别是一次函数
分别是一次函数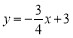 与
与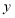 轴,
轴,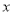 轴的交点,动点
轴的交点,动点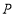 从点
从点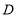 开始沿
开始沿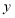 轴的正方向运动,运动的速度为2个单位长度/秒,设运动的时间为
轴的正方向运动,运动的速度为2个单位长度/秒,设运动的时间为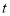 秒,以
秒,以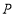 点为圆心,半径
点为圆心,半径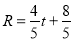 ,单位长度作圆,问:①当
,单位长度作圆,问:①当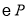 与直线
与直线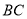 初次相切时,求此时运动的时间
初次相切时,求此时运动的时间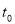 ;②当运动的时间
;②当运动的时间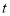 满足
满足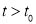 且
且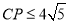 时,
时,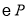 与直线
与直线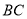 相交于
相交于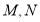 ,求弦长
,求弦长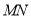 的最大值。
的最大值。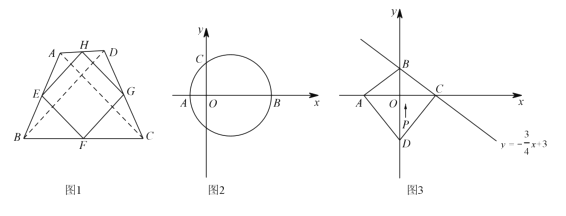
-
科目: 来源: 题型:
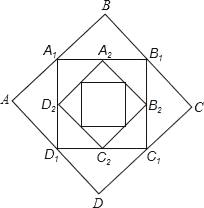
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,再顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…,以此类推,则第2018个正方形A2018B2018C2018D2018的周长是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,既是轴对称图形又是中心对称图形的是( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

