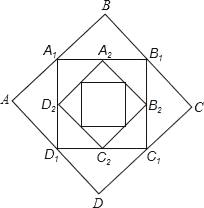
【题目】如图,正方形ABCD的边长为1,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,再顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…,以此类推,则第2018个正方形A2018B2018C2018D2018的周长是_____.
参考答案:
【答案】![]()
【解析】分析: 根据题意,利用中位线定理可证明顺次连接正方形ABCD四边中点得正方形A1B1C1D1的面积为正方形ABCD面积的一半,根据面积关系可得周长关系,以此类推可得正方形A2018B2018C2018D2018的周长.
详解: 顺次连接正方形ABCD四边的中点得正方形A1B1C1D1,则得正方形A1B1C1D1的面积为正方形ABCD面积的一半,即![]() ,则周长是原来的
,则周长是原来的![]() ;
;
顺次连接正方形A1B1C1D1中点得正方形A B C D ,则正方形A B C D 的面积为正方形A1B1C1D1面积的一半,即![]() ,则周长是原来的
,则周长是原来的![]() ;
;
顺次连接正方形A B C D 得正方形A B C D ,则正方形A B C D 的面积为正方形A B C D 面积的一半,即![]() ,则周长是原来的
,则周长是原来的![]() ;
;
顺次连接正方形A B C D 中点得正方形A4B4C4D4,则正方形A4B4C4D4的面积为正方形A B C D 面积的一半![]() ,则周长是原来的
,则周长是原来的![]() ;
;
以此类推,则第2018个正方形A2018B2018C2018D2018的周长是4×![]() =
=![]() ;
;
故答案是:![]() .
.
点睛: 本题考查了利用了三角形的中位线的性质,相似图形的面积比等于相似比的平方的性质.进而得到周长关系.
-
科目: 来源: 题型:
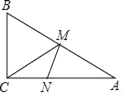
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=4,M是AB边上一动点,N是AC边上的一动点,则MN+MC的最小值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠A=90°,AB=AC=
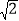 +2,D是边AC上的动点,BD的垂直平分线交BC于点E,连接DE,若△CDE为直角三角形,则BE的长为_____.
+2,D是边AC上的动点,BD的垂直平分线交BC于点E,连接DE,若△CDE为直角三角形,则BE的长为_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们约定:对角线相等的四边形称之为:“等线四边形”。
(1)①在“平行四边形、菱形、矩形、正方形”中一定是“等线四边形”的是___________________;
②如图1,若四边形
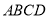 是“等线四边形”,
是“等线四边形”, 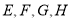 分别是边
分别是边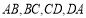 的中点,依次连接
的中点,依次连接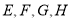 ,得到四边形
,得到四边形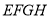 ,请判断四边形
,请判断四边形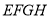 的形状:______________________;
的形状:______________________;(2)如图2,在平面直角坐标系
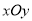 中,已知
中,已知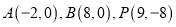 ,以
,以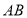 为直径作圆,该圆与
为直径作圆,该圆与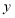 轴的正半轴交于点
轴的正半轴交于点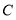 ,若
,若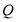 为坐标系中一动点,且四边形
为坐标系中一动点,且四边形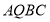 为“等线四边形”。当
为“等线四边形”。当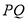 的长度最短时,求经过
的长度最短时,求经过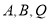 三点的抛物线的解析式;
三点的抛物线的解析式;(3)如图3,在平面直角坐标系
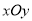 中,四边形
中,四边形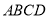 是“等线四边形”,
是“等线四边形”, 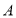 在
在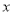 轴的负半轴上,
轴的负半轴上,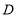 在
在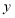 轴的负半轴上,且
轴的负半轴上,且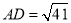 。点
。点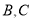 分别是一次函数
分别是一次函数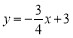 与
与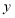 轴,
轴,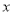 轴的交点,动点
轴的交点,动点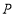 从点
从点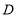 开始沿
开始沿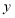 轴的正方向运动,运动的速度为2个单位长度/秒,设运动的时间为
轴的正方向运动,运动的速度为2个单位长度/秒,设运动的时间为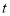 秒,以
秒,以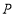 点为圆心,半径
点为圆心,半径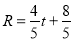 ,单位长度作圆,问:①当
,单位长度作圆,问:①当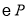 与直线
与直线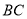 初次相切时,求此时运动的时间
初次相切时,求此时运动的时间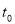 ;②当运动的时间
;②当运动的时间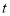 满足
满足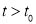 且
且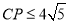 时,
时,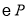 与直线
与直线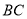 相交于
相交于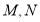 ,求弦长
,求弦长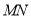 的最大值。
的最大值。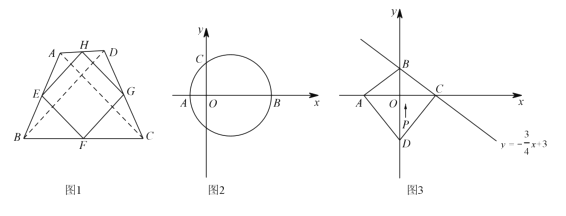
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,既是轴对称图形又是中心对称图形的是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BC的垂直平分线交AC于点E,交BC于点D,且AD=AB,连接BE交AD于点F,下列结论:( )
①∠EBC=∠C;②△EAF∽△EBA;③BF=3EF;④∠DEF=∠DAE,其中结论正确的个数有

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2 ;
(3)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标 .
相关试题

