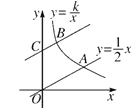
【题目】如图,直线![]() 与双曲线
与双曲线![]() (k>0,x>0)交于点A,将直线
(k>0,x>0)交于点A,将直线![]() 向上平移4个单位长度后,与y轴交于点C,与双曲线
向上平移4个单位长度后,与y轴交于点C,与双曲线![]() (k>0,x>0)交于点B,若OA=3BC,则k的值为( )
(k>0,x>0)交于点B,若OA=3BC,则k的值为( )
A. ![]() B.
B. ![]() C. 6 D. 3
C. 6 D. 3
参考答案:
【答案】A
【解析】分析: 先根据一次函数平移的性质求出平移后函数的解析式,再分别过点A、B作AD⊥x轴,BE⊥x轴,CF⊥BE于点F,再设A(3x,![]() x),由于OA=3BC,故可得出B(x,
x),由于OA=3BC,故可得出B(x,![]() x+4),再根据反比例函数中k=xy为定值求出x.
x+4),再根据反比例函数中k=xy为定值求出x.
详解: :∵将直线y=![]() x向上平移4个单位长度后,与y轴交于点C,
x向上平移4个单位长度后,与y轴交于点C,
∴平移后直线的解析式为y=![]() x+4,
x+4,
分别过点A、B作AD⊥x轴,BE⊥x轴,CF⊥BE于点F,设A(3x,![]() x),
x),
∵OA=3BC,BC∥OA,CF∥x轴,
∴△BCF∽△AOD,
∴CF=![]() OD,
OD,
∵点B在直线y=![]() x+4上,
x+4上,
∴B(x,![]() x+4),
x+4),
∵点A、B在双曲线y=![]() 上,
上,
∴3x![]() x=x(
x=x(![]() x+4),解得x=1,
x+4),解得x=1,
∴k=3×1×![]() ×1=
×1=![]() .
.
故选:A.
点睛: 本题考查的是反比例函数综合题,根据题意作出辅助线,设出A、B两点的坐标,再根据k=xy的特点求出k的值即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,由6相同的小正方体组合成的简单几何体.
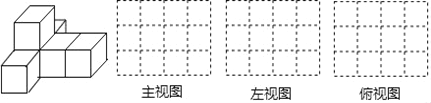
(1)请在方格纸中分别画出几何体的主视图、左视图和俯视图;
(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加 个小正方体.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系
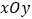 中,反比例函数图像与直线
中,反比例函数图像与直线 相交于横坐标为3的点A.
相交于横坐标为3的点A.(1)求反比例函数的解析式;
(2)如果点B在直线
 上,点C在反比例函数图像上,BC//
上,点C在反比例函数图像上,BC// 轴,BC= 4,且BC在点A上方,求点B的坐标.
轴,BC= 4,且BC在点A上方,求点B的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1.正方形ABCD,过点A作∠EAF=90°,两边分别交直线BC于点E,交线段CD于点F,G为AE中点,连接BG
(1)求证:△ABE≌△ADF
(2)如图2,过点G作BG的垂线交对角线AC于点H,求证:GH=GB;
(3)如图3,连接HF,若CH=3AH,AD=2
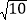 ,求线段HF的长.
,求线段HF的长.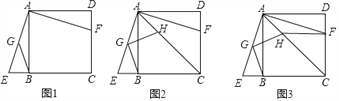
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板按如图方式摆放,∠1与∠2不一定互补的是( )
A.
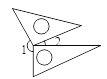 B.
B. 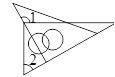 C.
C. 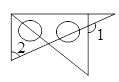 D.
D. 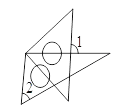
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(m,6),B(n,1)在反比例函数
 的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是_____________.
的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】货车在公路A处加满油后,以每小时60千米的速度匀速行驶,前往与A处相距360千米的B处.下表记录的是货车一次加满油后油箱剩余油量y(升)与行驶时间x(时)之间的关系:

(1)如果y关于x的函数是一次函数,求这个函数解析式(不要求写出自变量的取值范围)
(2)在(1)的条件下,如果货车的行驶速度和每小时的耗油量都不变,货车行驶4小时后到达C处,C的前方12千米的D处有一加油站,那么在D处至少加多少升油,才能使货车到达B处卸货后能顺利返回会D处加油?(根据驾驶经验,为保险起见,油箱内剩余油量应随时不少于10升)
相关试题

