【题目】已知:如图16,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式.
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.


参考答案:
【答案】(1)y=![]() x2+
x2+![]() x-3;(2) 当m=-2时,S四边形ABCD有最大值,最大值为
x-3;(2) 当m=-2时,S四边形ABCD有最大值,最大值为![]() ;(3)存在,点P的坐标为(-3,-3)或
;(3)存在,点P的坐标为(-3,-3)或![]() 或
或![]() .
.
【解析】
(1)先求出抛物线的对称轴,再由OC=3OB=3,a>0,即可求得C点坐标,由B(1,0)、C(0,-3)根据待定系数法即可求出函数解析式;
(2)过点D作DM∥y轴分别交线段AC和x轴于点M、N。先表示出四边形ABCD的面积,再求出直线AC的函数解析式,即可表示出DM的长,根据二次函数的性质即可得到结果;
分情况讨论:①过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,此时四边形ACP1E1为平行四边形,②如图②,平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,点B在抛物线y=ax2的图象上,则a的值为( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程(c+a)x2+2bx+(c-a)=0,其中a、b、c分别为△ABC三边的长.
(1)如果方程有两个相等的实数根,试判断△ABC的形状并说明理由;
(2)已知a:b:c=3:4:5,求该一元二次方程的根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰Rt△ABC,∠ACB=90°,CA=CB,以BC为边向外作等边△CBA,连接AD,过点C作∠ACB的角平分线与AD交于点E,连接BE.

(1)若AE=2,求CE的长度;
(2)以AB为边向下作△AFB,∠AFB=60°,连接FE,求证:FA+FB=
 FE.
FE. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
(1)求证:AB=AD;
(2)求证:CD平分∠ACE.
(3)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+3的图象经过点 (-3,0),(2,-5).
(1)试确定此二次函数的解析式;
(2)请你判断点P(-2,3)是否在这个二次函数的图象上?
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 与
与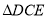 有公共顶点
有公共顶点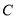 (顶点均按逆时针排列),
(顶点均按逆时针排列),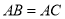 ,
,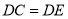 ,
,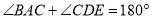 ,
,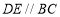 ,点
,点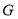 是
是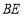 的中点,连接
的中点,连接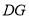 并延长交直线
并延长交直线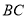 于点
于点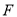 ,连接
,连接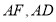 .
.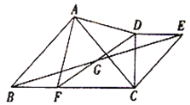
(1)如图,当
 时,
时,求证:①
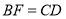 ;
;②
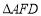 是等腰直角三角形.
是等腰直角三角形.(2)当
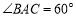 时,画出相应的图形(画一个即可),并直接指出
时,画出相应的图形(画一个即可),并直接指出 是何种特殊三角形.
是何种特殊三角形.
相关试题

