【题目】已知二次函数y=ax2+bx+3的图象经过点 (-3,0),(2,-5).
(1)试确定此二次函数的解析式;
(2)请你判断点P(-2,3)是否在这个二次函数的图象上?
参考答案:
【答案】(1)y=﹣x2﹣2x+3;(2)点P(﹣2,3)在这个二次函数的图象上,
【解析】
(1)根据给定点的坐标,利用待定系数法求出二次函数解析式即可;
(2)代入x=-2求出y值,将其与3比较后即可得出结论.
(1)设二次函数的解析式为y=ax2+bx+3;
∵二次函数的图象经过点(﹣3,0),(2,﹣5),则有:
![]()
解得;![]()
∴y=﹣x2﹣2x+3.
(2)把x=-2代入函数得y=﹣(﹣2)2﹣2×(﹣2)+3=﹣4+4+3=3,
∴点P(﹣2,3)在这个二次函数的图象上,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰Rt△ABC,∠ACB=90°,CA=CB,以BC为边向外作等边△CBA,连接AD,过点C作∠ACB的角平分线与AD交于点E,连接BE.

(1)若AE=2,求CE的长度;
(2)以AB为边向下作△AFB,∠AFB=60°,连接FE,求证:FA+FB=
 FE.
FE. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图16,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式.
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
(1)求证:AB=AD;
(2)求证:CD平分∠ACE.
(3)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】
 与
与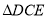 有公共顶点
有公共顶点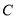 (顶点均按逆时针排列),
(顶点均按逆时针排列),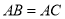 ,
,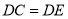 ,
,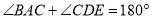 ,
,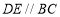 ,点
,点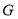 是
是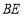 的中点,连接
的中点,连接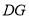 并延长交直线
并延长交直线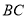 于点
于点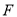 ,连接
,连接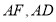 .
.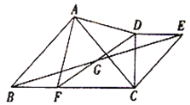
(1)如图,当
 时,
时,求证:①
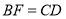 ;
;②
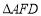 是等腰直角三角形.
是等腰直角三角形.(2)当
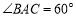 时,画出相应的图形(画一个即可),并直接指出
时,画出相应的图形(画一个即可),并直接指出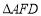 是何种特殊三角形.
是何种特殊三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:
(甲)作AB的中垂线,交BC于P点,则P即为所求;
(乙)以B为圆心,AB长为半径画弧,交BC于P点,则P即为所求.
对于两人的作法,下列判断何者正确?( )

A. 两人皆正确B. 两人皆错误C. 甲正确,乙错误D. 甲错误,乙正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小聪遇到这样一个有关角平分线的问题:如图1,在
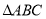 中,
中,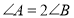 ,
,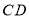 平分
平分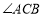 ,
,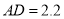 ,
,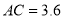 ,求
,求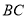 的长.
的长.小聪思考:因为
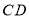 平分
平分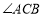 ,所以可在
,所以可在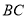 边上取点
边上取点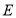 ,使
,使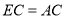 ,连接
,连接 .这样很容易得到
.这样很容易得到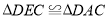 ,经过推理能使问题得到解决(如图2).
,经过推理能使问题得到解决(如图2).请回答:(1)
 是 三角形.
是 三角形.(2)
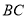 的长为 .
的长为 .参考小聪思考问题的方法,解决问题:
(3)如图3,已知
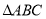 中,
中,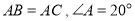 ,
, 平分
平分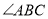 ,
,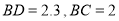 .求
.求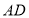 的长.
的长.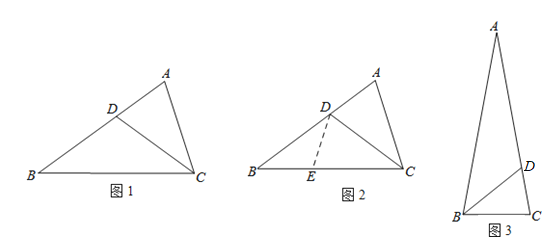
相关试题

