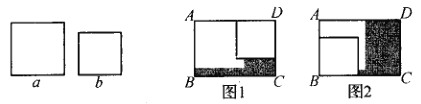
【题目】在长方形![]() 内,将两张边长分别为
内,将两张边长分别为![]() 和
和![]() 的正方形纸片按如图,如图两种方式放置(如图,如图中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设如图1中阴影部分的面积为
的正方形纸片按如图,如图两种方式放置(如图,如图中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设如图1中阴影部分的面积为![]() ,如图2中阴影部分的面积为
,如图2中阴影部分的面积为![]() .当
.当![]() 时,
时,![]() 的值为( )
的值为( )
A. 0B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】D
【解析】
利用面积的和差分别表示出S1和S2,然后利用整式的混合运算计算它们的差.
解:∵S1=(AB-a)a+(CD-b)(AD-a)=(AB-a)a+(AB-b)(AD-a),
S2=AB(AD-a)+(a-b)(AB-a),![]()
∴S2-S1
=AB(AD-a)+(a-b)(AB-a)-(AB-a)a-(AB-b)(AD-a)
=(AD-a)(AB-AB+b)+(AB-a)(a-b-a)
=bAD-ab-bAB+ab=b(AD-AB)
=3b.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
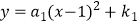 (a1>0)与抛物线
(a1>0)与抛物线 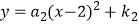 (a2<0)都经过y轴正半轴上的点A.过点A作x轴的平行线,分别与这两条抛物线交于B、C两点,以BC为边向下作等边△BCD,则△BCD的面积为 .
(a2<0)都经过y轴正半轴上的点A.过点A作x轴的平行线,分别与这两条抛物线交于B、C两点,以BC为边向下作等边△BCD,则△BCD的面积为 . 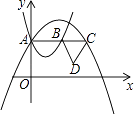
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为
 ,
, ,
, ,
, ,那么可以转换为该生所在班级序号,其序号为
,那么可以转换为该生所在班级序号,其序号为 .如图2第一行数字从左到右依次为0,1,0,1,序号为
.如图2第一行数字从左到右依次为0,1,0,1,序号为 ,表示该生为5班学生.表示6班学生的识别图案是( )
,表示该生为5班学生.表示6班学生的识别图案是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的验证方法.如图,火柴盒的一个侧面
 倒下到
倒下到 的位置,连接
的位置,连接 ,设
,设 、
、 、
、 ,请利用四边形
,请利用四边形 的面积验证勾股定理.
的面积验证勾股定理. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
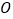 为等边三角形
为等边三角形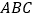 内一点,连接
内一点,连接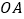 ,
,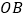 ,
,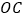 ,以
,以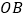 为一边作
为一边作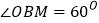 ,且
,且 ,连接
,连接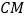 、
、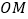 .
. (1)判断
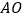 与
与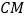 的大小关系并证明;
的大小关系并证明; (2)若
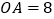 ,
,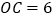 ,
,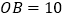 ,判断
,判断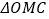 的形状并证明.
的形状并证明.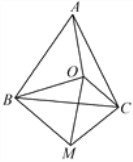
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校对初三学生进行物理、化学实验操作能力测试.物理、化学各有3个不同的操作实验题目,物理实验分别用①、②、③表示,化学实验分别用a、b、c表示.测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定,第一次抽签确定物理实验题目,第二次抽签确定化学实验题目.王刚同学对物理的①、②号实验和化学的b、c号实验准备得较好.请用画树状图(或列表)的方法,求王刚同学同时抽到两科都准备得较好的实验题目的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有甲、乙两个空调安装队分别为A、B两个公司安装空调,甲安装队为A公司安装66台空调,乙安装队为B公司安装60台空调,甲、乙两队安装空调所用的总时间相同.已知甲队比乙队平均每天多安装2台空调,求甲、乙两个安装队平均每天各安装空调的台数.
相关试题

