搜索
【题目】求若干个相同的不为零的有理数的除法运算叫做除方.
如：2÷2÷2，(-3)÷(-3)÷(-3 )÷( -3)等. 类比有理数的乘方，我们把 2÷2÷2 记作 2③，读作“2 的圈 3 次方”. (-3)÷(-3)÷(-3 )÷( -3)记作(-3)④，读作“-3 的圈 4 次方”.
一般地，把
（a≠0）记作
，读作“a的圈n次方”.
(1)直接写出计算结果： 
_____， 
_________， 
___________，
(2)我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，
请尝试将有理数的除方运算转化为乘方运算，归纳如下：一个非零有理数的圈 n 次方等于_____.
(3)计算 
.
参考答案：
【答案】（1）
， 
，-8；（2）它的倒数的n-2次方；（3）－1.
【解析】试题分析：（1）根据题中的新定义计算即可得到结果；
（2）归纳总结得到规律即可；
（3）利用得出的结论计算即可得到结果．
试题解析：解：（1）
， 
，﹣8；
（2）这个数倒数的（n﹣2）次方；
（3）24÷23+（﹣8）×2③
=24÷8+（﹣8）×
=3+（﹣4）
=﹣1．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在等腰直角△ABC中，∠ACB=90°，CO⊥AB于点O，点D、E分别在边AC、BC上，且AD=CE，连结DE交CO于点P，给出以下结论：
①△DOE是等腰直角三角形；②∠CDE=∠COE；③若AC=1，则四边形CEOD的面积为
；④AD2+BE2﹣2OP2=2DPPE，其中所有正确结论的序号是
-
科目： 来源： 题型：
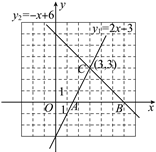
查看答案和解析>>【题目】已知一次函数y1＝2x－3，y2＝－x＋6在同一直角坐标系中的图象如图所示，它们的交点坐标为C(3，3)．
(1)根据图象指出x为何值时，y1＞y2；x为何值时，y1＜y2.
(2)求这两条直线与x轴所围成的△ABC的面积．
-
科目： 来源： 题型：
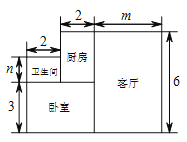
查看答案和解析>>【题目】小王购买了一套一居室，他准备将房子的地面铺上地砖，地面结构如图所示，根据图中所给的数据（单位：米），解答下列问题：
（1）用含
的代数式表示地面的总面积 
；
（2）已知
，且客厅面积是卫生间面积的 
倍，如果铺 
平方米地砖的平均费用为 
元，那么小王铺地砖的总费用为多少元? -
科目： 来源： 题型：
查看答案和解析>>【题目】今年4月初，某地连续降雨导致该地某水库水位持续上涨，下表是该水库4月1日～4月4日的水位变化情况：
日期x
1
2
3
4
水位y(米)
20.0
20.5
21.0
21.5
(1)请建立该水库水位y(米)与日期x之间的函数模型，求出函数表达式；
(2)请用求出的函数表达式预测该水库今年4月6日的水位；
(3)你能用求出的函数表达式预测该水库今年12月1日的水位吗？请简要说明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】近几年来，国家对购买新能源汽车实行补助政策，2016年某省对新能源汽车中的“插电式混合动力汽车”实行每辆3万元的补助，小刘对该省2016年“纯电动乘用车”和“插电式混合动力车”的销售计划进行了研究，绘制出如图所示的两幅不完整的统计图．
（1）补全条形统计图；
（2）求出“D”所在扇形的圆心角的度数；
（3）为进一步落实该政策，该省计划再补助4.5千万元用于推广上述两大类产品，请你预测，该省16年计划大约共销售“插电式混合动力汽车”多少辆？
注：R为纯电动续航行驶里程，图中A表示“纯电动乘用车”（100km≤R＜150km），B表示“纯电动乘用车”（150km≤R＜250km），C表示“纯电动乘用车”（R≥250km），D为“插电式混合动力汽车”． -
科目： 来源： 题型：
查看答案和解析>>【题目】某大型企业为了保护环境，准备购买A、B两种型号的污水处理设备共8台，用于同时治理不同成分的污水，若购买A型2台、B型3台需54万，购买A型4台、B型2台需68万元．
（1）求出A型、B型污水处理设备的单价；
（2）经核实，一台A型设备一个月可处理污水220吨，一台B型设备一个月可处理污水190吨，如果该企业每月的污水处理量不低于1565吨，请你为该企业设计一种最省钱的购买方案．
相关试题
