【题目】如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AECF是正方形?

参考答案:
【答案】(1)证明见解析;(2)当点O运动到AC的中点时,四边形AECF是矩形.(3)当点O是AC的中点,△ABC中∠ACB=90°时,四边形AECF是正方形.
【解析】试题解析:(1)根据平行线性质和角平分线性质及,由平行线所夹的内错角相等易证;
(2)当点O运动到AC的中点时,四边形AECF是矩形,根据矩形的判定方法,即一个角是直角的平行四边形是矩形可证.
(3))由OE=OF,OA=OC可判断四边形AECF为平行四边形,再证明∠ECF=90°,则可判断四边形AECF为矩形,根据正方形的判定方法,当∠2=45°时,四边形AECF为正方形,于是可得∠ACB=90°.
试题解析:(1)证明:∵CE平分∠ACB,
∴∠1=∠2,
又∵MN∥BC,
∴∠1=∠3,
∴∠3=∠2,
∴EO=CO,
同理,FO=CO,
∴EO=FO;
(2)解:当点O运动到AC的中点时,四边形AECF是矩形.
理由如下:
∵EO=FO,点O是AC的中点.
∴四边形AECF是平行四边形,
∵CF平分∠BCA的外角,
∴∠4=∠5,
又∵∠1=∠2,
∴∠2+∠4=![]() ×180°=90°.
×180°=90°.
即∠ECF=90度,
∴四边形AECF是矩形.
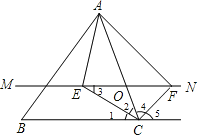
(3)∵OE=OF,OA=OC,
∴四边形AECF为平行四边形,
∵CE平分∠ACB,CF平分∠ACB的外角,
∴∠ECF=90°,
∴四边形AECF为矩形,
当∠2=45°时,四边形AECF为正方形,
此时∠ACB=90°,
即当点O是AC的中点,△ABC中∠ACB=90°时,四边形AECF是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系内,已知点(1-2a,a-2)在第三象限的角平分线上,求a的值及点的坐标?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a∥b,a∥c,那么b与c的位置关系是( )
A. 不一定平行 B. 一定平行 C. 一定不平行 D. 以上都有可能
-
科目: 来源: 题型:
查看答案和解析>>【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
【特例探究】
(1)如图1,当tan∠PAB=1,c=4
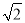 时,a= ,b= ;
时,a= ,b= ;如图2,当∠PAB=30°,c=2时,a= ,b= ;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
【拓展证明】
(3)如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3
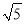 ,AB=3,求AF的长.
,AB=3,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式x2+ax+8和多项式x2﹣3x+b相乘的积中不含x3和x项的系数,求a和b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】假如火车票上的车次号有两个意义,一是数字越小表示车速越快,1~98次为特快列车,101~198次为直快列车,301~398次为普快列车,401~598次为普客列车;二是单数与双数表示不同的行驶方向,其中单数表示从北京开出,双数表示开往北京.根据以上规定,杭州开往北京的某一直快列车的车次号可能是( )
A. 200 B. 119 C. 120 D. 319
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
相关试题

