【题目】把二次函数y=a(x-h)2+k的图象先向左平移2个单位,再向上平移4个单位,得到二次函数y=![]() (x+1)2-1的图象.
(x+1)2-1的图象.
(1)试确定a,h,k的值;
(2)指出二次函数y=a(x-h)2+k的开口方向,对称轴和顶点坐标.
参考答案:
【答案】(1)a=![]() ,h=1,k=-5;(2)开口向上,对称轴为x=1,顶点坐标为(1,-5).
,h=1,k=-5;(2)开口向上,对称轴为x=1,顶点坐标为(1,-5).
【解析】试题分析:(1)二次函数的平移,可以看作是将二次函数y=![]() (x+1)2-1先向右平移2个单位,再向下平移4个单位得到二次函数y=a(x-h)2+k,然后再按二次函数图象的平移法则,确定函数解析式,即可得到结论;
(x+1)2-1先向右平移2个单位,再向下平移4个单位得到二次函数y=a(x-h)2+k,然后再按二次函数图象的平移法则,确定函数解析式,即可得到结论;
(2),直接根据函数解析式,结合二次函数的性质,进行回答即可.
试题分析:(1)∵二次函数y=a(x-h)2+k的图象先向左平移2个单位,再向上平移4个单位,得到二次函数y=![]() (x+1)2-1,
(x+1)2-1,
∴可以看作是将二次函数y=![]() (x+1)2-1先向右平移2个单位,再向下平移4个单位得到二次函数y=a(x-h)2+k,
(x+1)2-1先向右平移2个单位,再向下平移4个单位得到二次函数y=a(x-h)2+k,
而将二次函数y=![]() (x+1)2-1先向右平移2个单位,再向下平移4个单位得到二次函数为:y=
(x+1)2-1先向右平移2个单位,再向下平移4个单位得到二次函数为:y=![]() (x-1)2-5,
(x-1)2-5,
∴a=![]() ,b=1,k=-5;
,b=1,k=-5;
(2)二次函数y=![]() (x-1)2-5,
(x-1)2-5,
开口向上,对称轴为x=1,顶点坐标为(1,-5).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
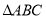 中,
中,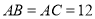 厘米,
厘米,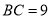 厘米,点
厘米,点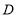 为
为 的中点.
的中点.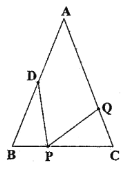
(1)如果点
 在线段
在线段 上以
上以 厘米
厘米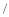 秒的速度由
秒的速度由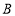 向
向 点运动,同时点
点运动,同时点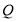 在线段
在线段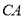 上由
上由 点向
点向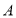 点运动.
点运动.①若点
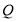 的运动速度与点
的运动速度与点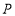 的运动速度相等,
的运动速度相等,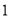 秒钟时,
秒钟时,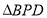 与
与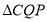 是否全等?请说明理由;
是否全等?请说明理由;②点
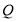 的运动速度与点
的运动速度与点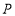 的运动速度不相等,当点
的运动速度不相等,当点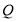 的运动速度为多少时,能够使
的运动速度为多少时,能够使 ?并说明理由;
?并说明理由;(2)若点
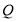 以②中的运动速度从点
以②中的运动速度从点 出发,点
出发,点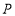 以原来运动速度从点
以原来运动速度从点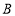 同时出发,都逆时针沿
同时出发,都逆时针沿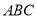 的三边运动,求多长时间点
的三边运动,求多长时间点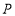 与点
与点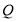 第一次在
第一次在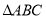 的哪条边上相遇?
的哪条边上相遇? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,AD 是 BC 边上的高,且∠ACB=∠BAD,AE 平分∠CAD,交 BC于点 E,过点 E 作 EF∥AC,分别交 AB、AD 于点 F、G.则下列结论:①∠BAC=90°;②∠AEF=∠BEF; ③∠BAE=∠BEA; ④∠B=2∠AEF,其中正确的有( )
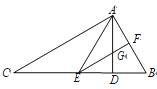
A. 4 个B. 3 个C. 2 个D. 1 个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 在
在 轴上,
轴上,  ,将线段
,将线段 绕点
绕点 顺时针旋转
顺时针旋转 ,使点
,使点 与点
与点 重合.
重合.(1)求点
 的坐标;
的坐标;(2)求经过
 、
、 、
、 三点的抛物线的解析式;
三点的抛物线的解析式;(3)在此抛物线的对称轴上,是否存在点
 ,使得以点
,使得以点 、
、 、
、 为顶点的三角形是等腰三角形?若存在,求出点
为顶点的三角形是等腰三角形?若存在,求出点 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当路况良好时,在干燥的路面上,汽车的刹车距离s与车速v之间的关系如下表所示:
v/(km/h)
40
60
80
100
120
s/m
2
4.2
7.2
11
15.6
(1)在平面直角坐标系中描出每对(v,s)所对应的点,并用光滑的曲线顺次连接各点。
(2)利用图象验证刹车距离s(m)与车速v(km/h)是否有如下关系:
 。
。(3)求当s=9m时的车速v。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知一次函数
 (k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数
(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数 (m≠0)的图象在第一象限交于C点,CD垂直于x轴,垂足为D.若OA=OB=OD=1.
(m≠0)的图象在第一象限交于C点,CD垂直于x轴,垂足为D.若OA=OB=OD=1.
(1)求点A、B、D的坐标;
(2)求一次函数和反比例函数的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】张强在一次投掷铅球时,刚出手时铅球离地面
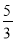 m,铅球运行的水平距离为4m时,达到最高,高度为3m,如图5所示:
m,铅球运行的水平距离为4m时,达到最高,高度为3m,如图5所示: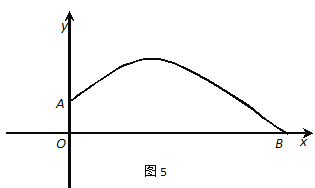
(1)请确定这个抛物线的顶点坐标
(2)求抛物线的函数关系式
(3)张强这次投掷成绩大约是多少?
相关试题

