【题目】如图,已知A,B分别为数轴上的两点,点A表示的数是﹣30,点B表示的数是50.
![]()
(1)请写出线段AB中点M表示的数是 .
(2)现有一只蚂蚁P从点B出发,以每秒3个单位长度的速度沿数轴向左移动,同时另一只蚂蚁Q恰好从点A出发,以每秒2个单位长度的速度沿数轴向右移动,设两只蚂蚁在数轴上的点C相遇.
①求A、B两点间的距离;
②求两只蚂蚁在数轴上的点C相遇时所用的时间;
③求点C对应的数是多少?
(3)若蚂蚁P从点B出发,以每秒3个单位长度的速度沿数轴向左运动,同时另一只蚂蚁恰好从A点出发,以每秒2个单位长度的速度沿数轴也向左运动,设两只蚂蚁在数轴上的D点相遇,求D点表示的数是多少?
参考答案:
【答案】(1)10;(2)①80;②16秒;③2;(3)-190.
【解析】
首先计算出AB长度,再根据中点平分线段可得点M表示的数;
①A、B间的距离用两点表示的数进行加减运算即可得;
②用路程除以速度即可表示时间;
③用50减去蚂蚁P的爬行路程即可得;
(3)设两只蚂蚁t秒后相遇,由题意得:定在A点左侧相遇,根据等量关系列出方程,然后可计算出运动时间,再根据A点表示的数,进而可得D点对应的数.
解:(1)AB=50+(﹣30)=20
∴AB中点M表示的数是10.
故答案为:10
(2)①A、B两点间的距离为:50﹣(﹣30)=80
②两只蚂蚁在数轴上的点C相遇时所用的时间为:80÷(3+2)=16(秒)
③点C对应的数是:50﹣16×3=2
(3)设两只蚂蚁t秒后相遇,可得: 2t+80=3t
解得 t=80
故 D点表示的数是:-( ![]() )-30=﹣190.
)-30=﹣190.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式
B.平方差公式
C.两数和的完全平方公式
D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 ,OB,OM,ON是
,OB,OM,ON是 内的射线.
内的射线. 如图1,若OM平分
如图1,若OM平分 ,ON平分
,ON平分 当射线OB绕点O在
当射线OB绕点O在 内旋转时,
内旋转时, ______度
______度
 也是
也是 内的射线,如图2,若
内的射线,如图2,若 ,OM平分
,OM平分 ,ON平分
,ON平分 ,当
,当 绕点O在
绕点O在 内旋转时,求
内旋转时,求 的大小.
的大小. 在
在 的条件下,若
的条件下,若 ,当
,当 在
在 绕O点以每秒
绕O点以每秒 的速度逆时针旋转t秒,如图3,若
的速度逆时针旋转t秒,如图3,若 :
: :3,求t的值.
:3,求t的值.
-
科目: 来源: 题型:
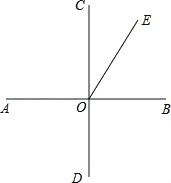
查看答案和解析>>【题目】如图,AB垂直CD(即∠AOC=∠AOD=∠BOD=∠BOC=90°)
(1)比较∠AOD,∠EOB,∠AOE大小(用“<”连接)
(2)如∠EOC=28°,求∠EOB和∠EOD的度数(适当写出解题过程)
-
科目: 来源: 题型:
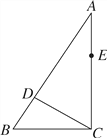
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在反比例函数y=
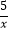 (x>0)的图象上有点P1、P2、P3、P4 , P5 , 它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , S4 , 则S1+S2+S3+S4的值为( )
(x>0)的图象上有点P1、P2、P3、P4 , P5 , 它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , S4 , 则S1+S2+S3+S4的值为( ) 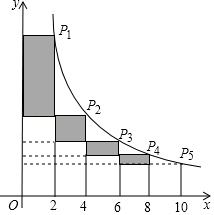
A.4.5
B.4.2
C.4
D.3.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( )

A.20
B.25
C.30
D.40
相关试题

