【题目】已知二次函数y=﹣x2+2x+m的部分图象如图所示,则关于x的一元二次方程﹣x2+2x+m=0的解为 . 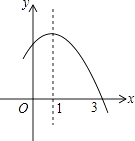
参考答案:
【答案】x1=﹣1或x2=3
【解析】解:依题意得二次函数y=﹣x2+2x+m的对称轴为x=1,与x轴的一个交点为(3,0),
∴抛物线与x轴的另一个交点横坐标为1﹣(3﹣1)=﹣1,
∴交点坐标为(﹣1,0)
∴当x=﹣1或x=3时,函数值y=0,
即﹣x2+2x+m=0,
∴关于x的一元二次方程﹣x2+2x+m=0的解为x1=﹣1或x2=3.
所以答案是:x1=﹣1或x2=3.
【考点精析】掌握抛物线与坐标轴的交点是解答本题的根本,需要知道一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,当ab>0时,函数y=ax2与函数y=bx+a的图象大致是( )
A.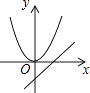
B.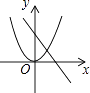
C.
D.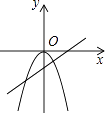
-
科目: 来源: 题型:
查看答案和解析>>【题目】在二次函数y=﹣(x﹣1)2+2的图象中,若y随x的增大而增大,则x的取值范围是( )
A.x>﹣1B.x<1C.x<﹣1D.x>1
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论正确的是( )
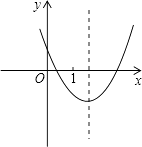
A.ac<0
B.当x=1时,y>0
C.方程ax2+bx+c=0(a≠0)有两个大于1的实数根
D.存在一个大于1的实数x0 , 使得当x<x0时,y随x的增大而减小;当x>x0时,y随x的增大而增大 -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
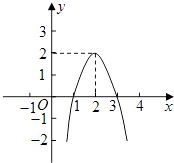
(1)写出方程ax2+bx+c=0的两个根;
(2)写出y随x的增大而减小的自变量x的取值范围;
(3)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:﹣2(﹣x2+5+4x)﹣(2x2﹣4﹣5x),其中x=﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为菱形,AB=BD,点B、C、D、G四个点在同一个圆⊙O上,连接BG 并延长交AD于点F,连接DG并延长交AB于点E,BD与CG交于点H,连接FH,下列结 论:①AE=DF;②FH∥AB;③△DGH∽△BGE;④当CG为⊙O的直径时,DF=AF.其中正确结论的个数是( )
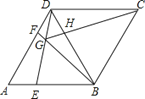
A. 1 B. 2 C. 3 D. 4
相关试题

