【题目】( ![]() ﹣
﹣ ![]() )÷
)÷ ![]() ,其中a=2017°+(﹣
,其中a=2017°+(﹣ ![]() )﹣1+
)﹣1+ ![]() tan30°.
tan30°.
参考答案:
【答案】解:原式= ![]() ×
× ![]() ﹣
﹣ ![]() ×
× ![]() =
= ![]() ﹣
﹣ 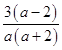
= ![]()
由于a=2017°+(﹣ ![]() )﹣1+
)﹣1+ ![]() tan30°,
tan30°,
∴a=1﹣5+3=﹣1
∴原式=﹣ ![]() =﹣2
=﹣2
【解析】先化简分式,然后再化简a的值,从而可求出原式的值.
【考点精析】利用零指数幂法则和整数指数幂的运算性质对题目进行判断即可得到答案,需要熟知零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下的一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.

(1)猜想与计算:
邻边长分别为3和5的平行四边形是阶准菱形;已知ABCD的邻边长分别为a,b(a>b),满足a=8b+r,b=5r,请写出ABCD是阶准菱形.
(2)操作与推理:
小明为了剪去一个菱形,进行了如下操作:如图2,把ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F处,得到四边形ABFE.请证明四边形ABFE是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+2过点A(﹣2,0),B(2,2),与y轴交于点C.
(1)求抛物线y=ax2+bx+2的函数表达式;
(2)若点D在抛物线y=ax2+bx+2的对称轴上,求△ACD的周长的最小值;
(3)在抛物线y=ax2+bx+2的对称轴上是否存在点P,使△ACP是直角三角形?若存在直接写出点P的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为4的菱形ABCD纸片折叠,使点A恰好落在对角线的交点O处,若折痕EF=2
 ,则∠A=( )
,则∠A=( ) 
A.120°
B.100°
C.60°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】2017赤峰)已知平行四边形ABCD.

(1)尺规作图:作∠BAD的平分线交直线BC于点E,交DC延长线于点F(要求:尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,求证:CE=CF. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了增强中学生的体质,某校食堂每天都为学生提供一定数量的水果,学校李老师为了了解学生喜欢吃哪种水果,进行了抽样调查,调查分为五种类型:A喜欢吃苹果的学生;B喜欢吃桔子的学生;C.喜欢吃梨的学生;D.喜欢吃香蕉的学生;E喜欢吃西瓜的学生,并将调查结果绘制成图1和图2 的统计图(不完整).请根据图中提供的数据解答下列问题:

(1)求此次抽查的学生人数;
(2)将图2补充完整,并求图1中的x;
(3)现有5名学生,其中A类型3名,B类型2名,从中任选2名学生参加体能测试,求这两名学生为同一类型的概率(用列表法或树状图法) -
科目: 来源: 题型:
查看答案和解析>>【题目】王浩同学用木板制作一个带有卡槽的三角形手机架,如图1所示.已知AC=20cm,BC=18cm,∠ACB=50°,王浩的手机长度为17cm,宽为8cm,王浩同学能否将手机放入卡槽AB内?请说明你的理由.(提示:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2)

相关试题

