【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动(
上运动(![]() 不与
不与![]() 、
、![]() 重合),连接
重合),连接![]() ,作
,作![]() ,
,![]() 交线段
交线段![]() 于
于![]() .
.

![]() 点
点![]() 从
从![]() 向
向![]() 运动时,
运动时,![]() 逐渐变________(填“大”或“小”);设
逐渐变________(填“大”或“小”);设![]() ,
,![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
![]() 当
当![]() 的长度是多少时,
的长度是多少时,![]() ,请说明理由;
,请说明理由;
![]() 在点
在点![]() 的运动过程中,
的运动过程中,![]() 的形状也在改变,当
的形状也在改变,当![]() 等于多少度时,
等于多少度时,![]() 是等腰三角形?判断并说明理由.
是等腰三角形?判断并说明理由.
参考答案:
【答案】小
【解析】试题分析:![]() 利用三角形的内角和即可得出结论;
利用三角形的内角和即可得出结论;
![]() 当
当![]() 时,利用
时,利用![]() ,
,![]() ,求出
,求出![]() ,再利用
,再利用![]() ,即可得出
,即可得出![]() ;
;
![]() 由于
由于![]() 的形状是等腰三角形.分三种情况讨论计算.
的形状是等腰三角形.分三种情况讨论计算.
试题解析:![]() 在
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
当点![]() 从点
从点![]() 向
向![]() 运动时,
运动时,![]() 增大,
增大,
∴![]() 减小;
减小;
![]() 当
当![]() 时,
时,![]() ,
,
理由:∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
在![]() 和
和![]() 中
中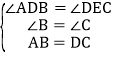 ,
,
∴![]() ;
;
![]() 当
当![]() 的度数为
的度数为![]() 或
或![]() 时,
时,![]() 的形状是等腰三角形,
的形状是等腰三角形,
理由:在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
①当![]() 时,
时,![]() ,
,
∴![]() ,不符合题意舍去,
,不符合题意舍去,
②当![]() 时,
时,![]() ,
,
根据三角形的内角和得,![]() ,
,
∴![]() ,
,
∴![]() ,
,
③当![]() 时,
时,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 的度数为
的度数为![]() 或
或![]() 时,
时,![]() 的形状是等腰三角形.
的形状是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明:
已知:如图,AB∥DE,求证:∠D+∠BCD﹣∠B=180°,
证明:过点C作CF∥AB.

∵AB∥CF(已知),
∴∠B= ( ).
∵AB∥DE,CF∥AB( 已知 ),
∴CF∥DE ( )
∴∠2+ =180° ( )
∵∠2=∠BCD﹣∠1,
∴∠D+∠BCD﹣∠B=180° ( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC内接于⊙O,过点A作直线EF.

(1)如图①,AB为直径,要使EF为⊙O的切线,还需添加的条件是(只需写出三种情况): ①;②;③ .
(2)如图②,AB是非直径的弦,∠CAE=∠B,求证:EF是⊙O的切线.
(3)如图③,AB是非直径的弦,∠CAE=∠ABC,EF还是⊙O的切线吗?若是,请说明理由;若不是,请解释原因. -
科目: 来源: 题型:
查看答案和解析>>【题目】某电脑公司开发出一种软件,从研发到年初上市后,经历了从亏损到盈利的过程,如图中的图象是抛物线的一段,它刻画了该软件上市以来累积利润S(万元)与销售时间t(月)之间的函数关系(即前t个月的利润总和S与t之间的函数关系),根据图象提供的信息,解答下列问题:

(1)该种软件上市第几个月后开始盈利?
(2)求累积利润S(万元)与时间t(月)之间的函数表达式;
(3)截止到几月末,公司累积利润达到30万元?
(4)求公司第6个月末所累积的利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=4,E,F分别是边BC,CD边上的动点,且AE=AF,设△AEF的面积为y,EC的长为x.

(1)求y与x之间的函数表达式,并写出自变量x的取值范围.
(2)当x取何值时,△AEF的面积最大,最大面积是多少?
(3)在直角坐标系中画出y关于x的函数的图象. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别为AC、AB的中点,连DE、CE.则下列结论中不一定正确的是( )

A.ED∥BC
B.ED⊥AC
C.∠ACE=∠BCE
D.AE=CE -
科目: 来源: 题型:
查看答案和解析>>【题目】如图中的图像(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在整个行驶过程中的平均速度为80.8千米/时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减小.⑤汽车离出发地64千米是在汽车出发后1.2小时时。其中正确的说法共有( )

A.1个 B.2个 C.3个 D.4个
相关试题

