【题目】如图,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,作正方形DEFG,连接AE,若BC=DE=2,将正方形DEFG绕点D逆时针方向旋转,在旋转过程中,当AE为最大值时,则AF的值_____________.

参考答案:
【答案】![]()
【解析】如图1,连接AD,BG,
∵在Rt△BAC中,AB=AC,D为斜边BC中点,
∴AD=BD,AD⊥BC,∴∠ADG+∠GDB=90°,
∵四边形EFGD为正方形,∴DE=DG,且∠GDE=90°,
∴∠ADG+∠ADE=90°,∴∠BDG=∠ADE,
在△BDG和△ADE中,∵BD=AD,∠BDG=∠ADE,GD=ED,
∴△BDG≌△ADE(SAS),∴BG=AE,
∴当BG取得最大值时,AE取得最大值,
如图2,当旋转角为270°时,此时BG最大,BG=AE,
∵BC=DE=2,∴BG=1+4=3.∴AE=3,
在Rt△AEF中,由勾股定理,得AF=![]() ,
,
故答案为: ![]() .
.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系xOy中,直线y=mx与双曲线
 相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1. 
(1)求m、n的值;
(2)求直线AC的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠A=60°,点E,F分别在AB,AC上,把∠A沿着EF对折,使点A落在BC上点D处,且使ED⊥BC.

(1)猜测AE与BE的数量关系,并说明理由;
(2)求证:四边形AEDF是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
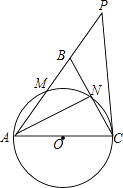
(1)求证:直线CP是⊙O的切线;
(2)若BC=2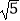 ,sin∠BCP=
,sin∠BCP= 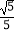 ,求点B到AC的距离.
,求点B到AC的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.

(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
(4)问:若抛物线顶点为D,点Q为直线AC上一动点,当△DOQ的周长最小时,求点Q的坐标 -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学对本校初2017届500名学生中中考参加体育加试测试情况进行调查,根据男生1000米及女生800米测试成绩整理,绘制成不完整的统计图,(图①,图②),请根据统计图提供的信息,回答下列问题:
(1)该校毕业生中男生有 人;扇形统计图中a= ;

(2)补全条形统计图;
(3)若500名学生中随机抽取一名学生,这名学生该项成绩在8分及8分以下的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于函数y=
 (x﹣6)2+3的图象,下列叙述错误的是( )
(x﹣6)2+3的图象,下列叙述错误的是( )
A.图象是抛物线,开口向上
B.对称轴为直线x=6
C.顶点是图象的最高点,坐标为(6,3)
D.当x<6时,y随x的增大而减小;当x>6时,y随x的增大而增大
相关试题

