【题目】如图,在Rt△ABC中,∠C=90°,∠A=60°,点E,F分别在AB,AC上,把∠A沿着EF对折,使点A落在BC上点D处,且使ED⊥BC. 
(1)猜测AE与BE的数量关系,并说明理由;
(2)求证:四边形AEDF是菱形.
参考答案:
【答案】
(1)解:AE= ![]() BE.理由如下:
BE.理由如下:
Rt△ABC中,∠A=60°,得∠B=30°.
则在Rt△BDE中有DE= ![]() BE.
BE.
由对折可知AE=DE,则AE= ![]() BE
BE
(2)证明:由∠C=90°,ED⊥BC得DE∥AC,
∴∠DFC=∠EDF=∠A=60°,
∴DF∥AE.
∴四边形AEDF是平行四边形.
又AE=ED,
∴平行四边形AEDF是菱形
【解析】(1)在Rt△ABC中,由直角三角形的性质:两锐角互余得∠B=30°,则在Rt△ADE中有DE=BEsin30°= ![]() BE,又由对折可知AE=DE,则AE=
BE,又由对折可知AE=DE,则AE= ![]() BE;(2)易得DE∥AC,所以∠DFC=∠EDF=∠A=60°,所以DF∥AE. 由两组对边分别平行的四边形是平行四边形得,四边形AEDF是平行四边形.
BE;(2)易得DE∥AC,所以∠DFC=∠EDF=∠A=60°,所以DF∥AE. 由两组对边分别平行的四边形是平行四边形得,四边形AEDF是平行四边形.
又AE=ED,所以邻边相等的平行四边形AEDF是菱形.
【考点精析】解答此题的关键在于理解菱形的判定方法的相关知识,掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级.现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出图所示的统计图,已知图中从左到右的四个长方形的高的比为:14:9:6:1,评价结果为D等级的有2人,请你回答以下问题: ①共抽测了人;②样本中B等级的频率是;
③如果要绘制扇形统计图,D等级在扇形统计图中所占的圆心角是度;
④该校九年级的毕业生共300人,假如“综合素质”等级为A或B的学生才能报考示范性高中,请你计算该校大约有名学生可以报考示范性高中.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵.两次共花费940元(两次购进的A、B两种花草价格均分别相同).
(1)A、B两种花草每棵的价格分别是多少元?
(2)若购买A、B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系xOy中,直线y=mx与双曲线
 相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1. 
(1)求m、n的值;
(2)求直线AC的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
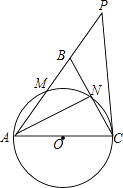
(1)求证:直线CP是⊙O的切线;
(2)若BC=2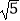 ,sin∠BCP=
,sin∠BCP= 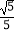 ,求点B到AC的距离.
,求点B到AC的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,作正方形DEFG,连接AE,若BC=DE=2,将正方形DEFG绕点D逆时针方向旋转,在旋转过程中,当AE为最大值时,则AF的值_____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.

(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
(4)问:若抛物线顶点为D,点Q为直线AC上一动点,当△DOQ的周长最小时,求点Q的坐标
相关试题

