【题目】如图,直角坐标系![]() 中,一次函数
中,一次函数![]() 的图像
的图像![]() 分别与
分别与![]() ,
,![]() 轴交于
轴交于![]() ,
,![]() 两点,正比例函数的图像
两点,正比例函数的图像![]() 与
与![]() 交于点
交于点![]()
![]() .
.

(1)求![]() 的值及
的值及![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)一次函数![]() 的图像为
的图像为![]() ,且
,且![]() ,
,![]() ,
,![]() 不能围成三角形,直接写出
不能围成三角形,直接写出![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)15;(3)
;(2)15;(3)![]() ,
,![]() ,
,![]() .
.
【解析】
(1)先求得点C的坐标,再运用待定系数法即可得到![]() 的解析式;
的解析式;
(2)过C作CD⊥AO于D,CE⊥BO于E,则CD=4,CE=2,再根据A(10,0),B(0,5),可得AO=10,BO=5,进而得出![]() 的值;
的值;
(3)分三种情况:当![]() 经过点C(2,4)时,
经过点C(2,4)时,![]() ;当
;当![]() ,
,![]() 平行时,k=2;当
平行时,k=2;当![]() ,
,![]() 平行时,
平行时,![]() ;故可以得到k的值.
;故可以得到k的值.
解:(1)把C(m,4)代入一次函数![]() ,可得
,可得![]() ,
,
解得m=2,
∴C(2,4),
设![]() 的解析式为
的解析式为![]() ,
,
则有![]() ,
,
解得![]() ,
,
∴![]() 的解析式为
的解析式为![]() ;
;
(2)
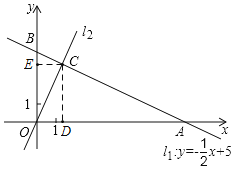
如图,过C作CD⊥AO于D,CE⊥BO于E,则CD=4,CE=2,
∵A,B两点在直线![]() 上,
上,
当x=0时, y=5;当y=0时, x=10,
即A的坐标为(10,0),B的坐标为(0,5),
∴AO=10,BO=5,
∴![]() .
.
(3)一次函数y=kx+1的图象为![]() ,且
,且![]() ,
,![]() ,
,![]() 不能围成三角形,
不能围成三角形,
∴分三种情况:
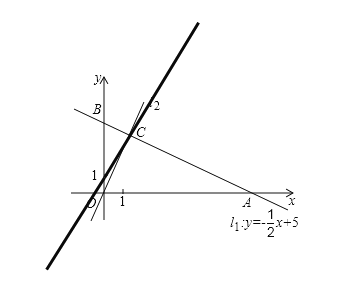
当![]() :
:![]() 经过点C(2,4)时,
经过点C(2,4)时,
得:![]() ;
;
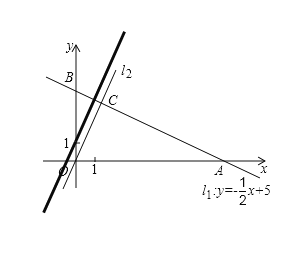
当![]() :
:![]() ,
,![]() :
:![]() 平行时,
平行时,
得:![]() ;
;
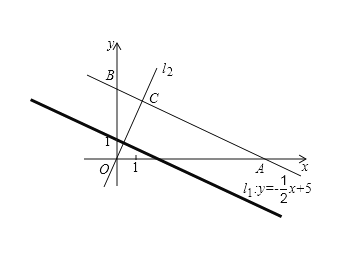
当:![]() :
:![]() ,
,![]() :
:![]() 平行时,
平行时,
![]() ;
;
故k的值可以为: ![]() ,
,![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年圣诞节前夕,小明、小丽两位同学到某超市调研一种袜子的销售情况,
这种袜子的进价为每双 1 元,请根据小丽提供的信息解决小明提出的问题.
小丽:每双定价 2 元,每天能卖出 500 双,而且这种袜子的售价每上涨 0.1 元,其每天的销售量将减少 10 双.
小明:照你所说,如果要实现每天 800 元的销售利润,那该如何定价?别忘了,物价局有规定,售价不能超过进价的 300%呦.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D是△ABC内部的一点,BD=CD,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,且BE=CF.求证:AB=AC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(﹣2,3)、B(4,3).C(﹣1,﹣3)

(1)点B到坐标原点的距离为 ;
(2)求BC的长;
(3)点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
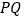 为圆
为圆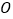 的直径,点
的直径,点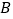 在线段
在线段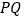 的延长线上,
的延长线上,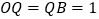 ,动点
,动点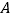 在圆
在圆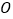 的上半圆上运动(包含
的上半圆上运动(包含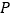 、
、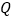 两点),以线段
两点),以线段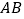 为边向上作等边三角形
为边向上作等边三角形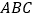 ,
,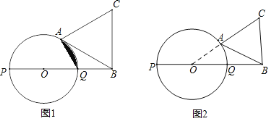
 当线段
当线段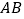 所在的直线与圆
所在的直线与圆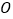 相切时,求阴影部分的面积(图
相切时,求阴影部分的面积(图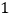 )
)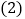 设
设 ,当线段
,当线段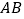 与圆
与圆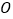 只有一个公共点(即
只有一个公共点(即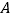 点)时,求
点)时,求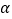 的范围(图
的范围(图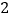 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】操作发现:如图,已知△ABC和△ADE均为等腰三角形,AB=AC,AD=AE,将这两个三角形放置在一起,使点B,D,E在同一直线上,连接CE.

(1)如图1,若∠ABC=∠ACB=∠ADE=∠AED=55°,求证:△BAD≌△CAE;
(2)在(1)的条件下,求∠BEC的度数;
拓广探索:(3)如图2,若∠CAB=∠EAD=120°,BD=4,CF为△BCE中BE边上的高,请直接写出EF的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.

(1)求证:△DAE≌△CFE;
(2)若AB=BC+AD,求证:BE⊥AF.
相关试题

