Question

【题目】如图，为圆的直径，点在线段的延长线上，，动点在圆的上半圆上运动（包含、两点），以线段为边向上作等边三角形，

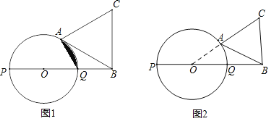
当线段所在的直线与圆相切时，求阴影部分的面积（图）

设，当线段与圆只有一个公共点（即点）时，求的范围（图）

Answer 1

【答案】（1）；当线段与圆只有一个公共点（即点）时，．

【解析】

（1）连结OA，如图1，由切线的性质得OA⊥BA，而OQ=BQ=1，于是根据直角三角形斜边上的中线性质得到AQ=OQ=BQ=1，所以△OAQ为等边三角形，得到∠AOQ=60°，然后根据扇形面积公式，利用S阴影部分=S扇形AOQ﹣S△AOQ进行计算；

（2）如图2，当点A在Q点时，易α=0°，当点A为切点，由（1）得α=60°，于是可判断线段AB与圆O只有一个公共点（即A点）时，0≤α≤60°．

（1）连结OA，如图1．

∵线段AB所在的直线与圆O相切，∴OA⊥BA．

∵OQ=BQ=1，∴AQ=OQ=BQ=1，∴△OAQ为等边三角形，∴∠AOQ=60°，∴S阴影部分=S扇形AOQ﹣S△AOQ=﹣×12=π﹣；

（2）如图2，当点A在Q点时，α=0°，当点A为线段AB的所在的直线与⊙O相切时切点，由（1）得α=60°，所以当线段AB与圆O只有一个公共点（即A点）时，0≤α≤60°．